The Personal Website of Mark W. Dawson

Containing His Articles, Observations, Thoughts, Meanderings,
and some would say Wisdom (and some would say not).

Chaos, Complexity, Networks, and Dynamic Science

1. Introduction
2. Chaos, Complexity, Network, and Dynamic Science
   1. Chaos
   2. Complexity
   3. Networks
   4. Dynamics
3. Observations on Chaos, Complexity, Networks, and Dynamics Science
   1. Chaos theory
   2. Complexity
   3. Network science
   4. Dynamic science
4. Examples of Chaos, Complexity, And Networks
   1. Simple - Planetary Network
   2. Intermediate  – Internet Routing
   3. Complex – Cell Phone Routing
   4. Dynamic - Social Network
5. Final Thoughts:
6. Further Readings
7. Disclaimer

Introduction

This article is an examination of the issues and concerns of Chaos, Complexity, and Network Science, and their impacts on Computer Models and Societal decision making. What are chaos, complexity, and network science, and what does it have to do with computer modeling and Societal decision making. Directly Nothing – Indirectly Everything! If you are going to utilize computer modeling, to determine future possibilities, or to decide or formulate a public policy based on computer modeling then you need to be aware of chaos, complexity, and network science. I will not delve into specific details of Chaos, Complexity, and Network Science, nor will I be utilizing any science or mathematics in discussing these issues and concerns. 

I should point out that I am NOT a scientist or engineer, nor have I received any education or training in science or engineering. This paper is the result of my readings on this subject in the past decades. Many academics, scientists, and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists and engineers’ entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. When writing for the general public this accuracy and thoroughness can often lead to less understandability. I believe it is essential for all laypersons to grasp the concepts of within this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.

Chaos, Complexity, Network, and Dynamic Science

We first need to understand something of chaos, complexity, networks, and dynamics theory to understand their impact on computer modeling and societal decisions.

Chaos

Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws, of dynamical systems, that are highly sensitive to initial conditions, that were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:

"Chaos: When the present determines the future, but the approximate present does not approximately determine the future."

An early proponent of chaos theory was Henri Poincaré. In the 1880s, while studying the three-body problem, he found that there can be orbits that are nonperiodic, and yet not forever increasing nor approaching a fixed point. In 1898 Jacques Hadamard published an influential study of the chaotic motion of a free particle gliding frictionlessly on a surface of constant negative curvature, called "Hadamard's billiards". Hadamard was able to show that all trajectories are unstable, in that all particle trajectories diverge exponentially from one another, with a positive Lyapunov exponent. Chaos theory began in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out by George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright and John Edensor Littlewood, and Stephen Smale] Except for Smale, these studies were all directly inspired by physics: the three-body problem in the case of Birkhoff, turbulence and astronomical problems in the case of Kolmogorov, and radio engineering in the case of Cartwright and Littlewood.[citation needed] Although chaotic planetary motion had not been observed, experimentalists had encountered turbulence in fluid motion and nonperiodic oscillation in radio circuits without the benefit of a theory to explain what they were seeing.

Despite initial insights in the first half of the twentieth century, chaos theory became formalized as such only after mid-century, when it first became evident to some scientists that linear theory, the prevailing system theory at that time, simply could not explain the observed behavior of certain experiments like that of the logistic map. What had been attributed to measure imprecision and simple "noise" was considered by chaos theorists as a full component of the studied systems.

The main catalyst for the development of chaos theory was the electronic computer. Much of the mathematics of chaos theory involves the repeated iteration of simple mathematical formulas, which would be impractical to do by hand. Electronic computers made these repeated calculations practical, while figures and images made it possible to visualize these systems. As a graduate student in Chihiro Hayashi's laboratory at Kyoto University, Yoshisuke Ueda was experimenting with analog computers and noticed, on November 27, 1961, what he called "randomly transitional phenomena". Yet his advisor did not agree with his conclusions at the time, and did not allow him to report his findings until 1970.

Edward Lorenz was an early pioneer of the theory. His interest in chaos came about accidentally through his work on weather prediction in 1961.Lorenz was using a simple digital computer, a Royal McBee LGP-30, to run his weather simulation. He wanted to see a sequence of data again, and to save time he started the simulation in the middle of its course. He did this by entering a printout of the data that corresponded to conditions in the middle of the original simulation. To his surprise, the weather the machine began to predict was completely different from the previous calculation. Lorenz tracked this down to the computer printout. The computer worked with 6-digit precision, but the printout rounded variables off to a 3-digit number, so a value like 0.506127 printed as 0.506. This difference is tiny, and the consensus at the time would have been that it should have no practical effect. However, Lorenz discovered that small changes in initial conditions produced large changes in long-term outcome. Lorenz's discovery, which gave its name to Lorenz attractors, showed that even detailed atmospheric modelling cannot, in general, make precise long-term weather predictions.

In 1963, Benoit Mandelbrot found recurring patterns at every scale in data on cotton prices. Beforehand he had studied information theory and concluded noise was patterned like a Cantor set: on any scale the proportion of noise-containing periods to error-free periods was a constant – thus errors were inevitable and must be planned for by incorporating redundancy. Mandelbrot described both the "Noah effect" (in which sudden discontinuous changes can occur) and the "Joseph effect" (in which persistence of a value can occur for a while, yet suddenly change afterwards). This challenged the idea that changes in price were normally distributed. In 1967, he published "How long is the coast of Britain? Statistical self-similarity and fractional dimension", showing that a coastline's length varies with the scale of the measuring instrument, resembles itself at all scales, and is infinite in length for an infinitesimally small measuring device. Arguing that a ball of twine appears as a point when viewed from far away (0-dimensional), a ball when viewed from fairly near (3-dimensional), or a curved strand (1-dimensional), he argued that the dimensions of an object are relative to the observer and may be fractional. An object whose irregularity is constant over different scales ("self-similarity") is a fractal (examples include the Menger sponge, the Sierpinski gasket, and the Koch curve or snowflake, which is infinitely long yet encloses a finite space and has a fractal dimension of circa 1.2619). In 1982 Mandelbrot published The Fractal Geometry of Nature, which became a classic of chaos theory. Biological systems such as the branching of the circulatory and bronchial systems proved to fit a fractal model.

Complexity

A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication systems, complex software and electronic systems, social and economic organizations (like cities), an ecosystem, a living cell, and ultimately the entire universe.

Complex systems are systems whose behavior is intrinsically difficult to model due to the dependencies, competitions, relationships, or other types of interactions between their parts or between a given system and its environment. Systems that are "complex" have distinct properties that arise from these relationships, such as nonlinearity, emergence, spontaneous order, adaptation, and feedback loops, among others. Because such systems appear in a wide variety of fields, the commonalities among them have become the topic of their independent area of research. In many cases, it is useful to represent such a system as a network where the nodes represent the components and links to their interactions.

The term complex systems often refers to the study of complex systems, which is an approach to science that investigates how relationships between a system's parts give rise to its collective behaviors and how the system interacts and forms relationships with its environment. The study of complex systems regards collective, or system-wide, behaviors as the fundamental object of study; for this reason, complex systems can be understood as an alternative paradigm to reductionism, which attempts to explain systems in terms of their constituent parts and the individual interactions between them.

As an interdisciplinary domain, complex systems draws contributions from many different fields, such as the study of self-organization and critical phenomena from physics, that of spontaneous order from the social sciences, chaos from mathematics, adaptation from biology, and many others. Complex systems is therefore often used as a broad term encompassing a research approach to problems in many diverse disciplines, including statistical physics, information theory, nonlinear dynamics, anthropology, computer science, meteorology, sociology, economics, psychology, and biology.

Networks

The study of Network Science has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this field is the famous Seven Bridges of Königsberg written by Leonhard Euler in 1736. Euler's mathematical description of vertices and edges was the foundation of graph theory, a branch of mathematics that studies the properties of pairwise relations in a network structure. The field of graph theory continued to develop and found applications in chemistry..

Dénes Konig, a Hungarian mathematician and professor, wrote the first book in Graph Theory, entitled "Theory of finite and infinite graphs", in 1936. In the 1930s Jacob Moreno, a psychologist in the Gestalt tradition, arrived in the United States. He developed the sociogram and presented it to the public in April 1933 at a convention of medical scholars. Moreno claimed that "before the advent of sociometry no one knew what the interpersonal structure of a group 'precisely' looked like (Moreno, 1953). The sociogram was a representation of the social structure of a group of elementary school students. The boys were friends of boys and the girls were friends of girls with the exception of one boy who said he liked a single girl. The feeling was not reciprocated. This network representation of social structure was found so intriguing that it was printed in The New York Times (April 3, 1933, page 17). The sociogram has found many applications and has grown into the field of social network analysis.

Probabilistic theory in network science developed as an offshoot of graph theory with Paul Erdos and Alfréd Rényi's eight famous papers on random graphs. For social networks the exponential random graph model or p* is a notational framework used to represent the probability space of a tie occurring in a social network. An alternate approach to network probability structures is the network probability matrix, which models the probability of edges occurring in a network, based on the historic presence or absence of the edge in a sample of networks.

In 1998, David Krackhardt and Kathleen Carley introduced the idea of a meta-network with the PCANS Model. They suggest that "all organizations are structured along these three domains, Individuals, Tasks, and Resources". Their paper introduced the concept that networks occur across multiple domains and that they are interrelated. This field has grown into another sub-discipline of network science called dynamic network analysis.

Dynamics

Dynamical Systems Theory and Dynamical Systems is an area of mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.

This theory deals with the long-term qualitative behavior of dynamical systems, and studies the nature of, and when possible the solutions of, the equations of motion of systems that are often primarily mechanical or otherwise physical in nature, such as planetary orbits and the behaviour of electronic circuits, as well as systems that arise in biology, economics, and elsewhere. Much of modern research is focused on the study of chaotic systems.

In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manifold. The evolution rule of the dynamical system is a function that describes what future states follow from the current state. Often the function is deterministic, that is, for a given time interval only one future state follows from the current state. However, some systems are stochastic, in that random events also affect the evolution of the state variables. In physics, a dynamical system is described as a "particle or ensemble of particles whose state varies over time and thus obeys differential equations involving time derivatives". In order to make a prediction about the system's future behavior, an analytical solution of such equations or their integration over time through computer simulation is realized. The study of dynamical systems is the focus of dynamical systems theory, which has applications to a wide variety of fields such as mathematics, physics, biology, chemistry, engineering, economics, history, and medicine. Dynamical systems are a fundamental part of chaos theory, logistic map dynamics, bifurcation theory, the self-assembly and self-organization processes, and the edge of chaos concept.

The concept of dynamical systems theory has its origins in Newtonian mechanics. There, as in other natural sciences and engineering disciplines, the evolution rule of dynamical systems is given implicitly by a relation that gives the state of the system only a short time into the future. Before the advent of fast computing machines, solving a dynamical system required sophisticated mathematical techniques and could only be accomplished for a small class of dynamical systems.

Observations on Chaos, Complexity, Networks, and Dynamics Science

Chaos theory

Chaos theory is the field of study in mathematics and science that studies the behavior and condition of dynamical systems that are highly sensitive to initial conditions, a response popularly referred to as the butterfly effect (Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?). Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general. This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions when no random elements are involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz (who discover it) as:

Chaos: When the present determines the future, but the approximate present does not approximately determine the future.

One meteorologist remarked that if the theory were correct, one flap of a sea gull's wings would be enough to alter the course of the weather forever. The controversy has not yet been settled, but the most recent evidence seems to favor the seagulls. Chaotic behavior exists in many natural systems, such as weather, climate, geology, celestial mechanics, and quantum theory. This behavior can be studied through analysis of a chaotic mathematical model, or through various analytical techniques. Chaos theory has applications in several disciplines, including meteorology, sociology, physics, computer science, engineering, economics, biology, and philosophy. What this means is that every so often, and at unknown times, the scientific predictions do not match the actual result. Edward Lorenz summarized his thoughts on Chaos as follows:

• Chaos does not only arise out of complexity, it arises even out of simplicity.
• Chaos doesn't usually emerge slowly, it leaps out at you.
• Chaotic behavior appears to be random but isn't really.

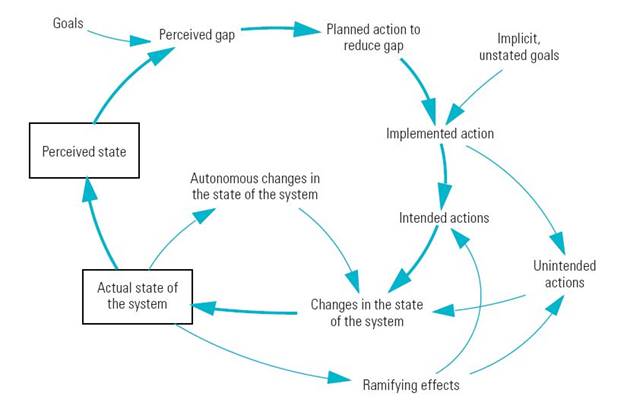
The following is Lorenz Diagram of a simple chaotic system:

Complexity

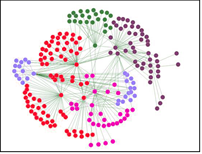
Complexity characterizes the behavior of a system or model whose components interact in multiple ways and follow local rules, meaning there are no reasonable means to define the various possible interactions. Complexity arises because some systems are very sensitive to their starting conditions so that a tiny difference in their initial starting conditions can cause big differences in where they end up. And many systems have a feedback into themselves that affects their own behavior, which leads to more complexity. Therefore, sensitivity and feedback lead to chaos and complexity, which leads to unpredictability (very unscientific). This can be seen in the diagram below.

Network science

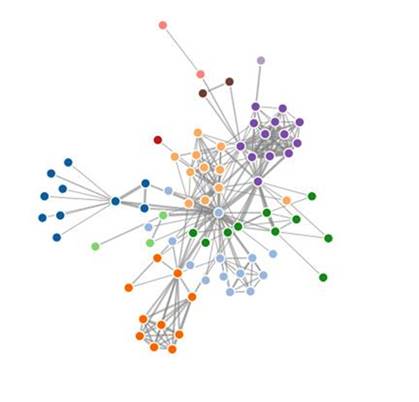
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks. Distinct elements or actors represented by nodes (known as vertices), and the links between the nodes (known as edges), define the Network Topology. A change in a vertices or an edge is propagated throughout the network and the Network Topology changes accordingly. Network science draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena. The science of networking has taken tremendous strides in the last two decades, as advanced computers have allowed the computer modeling of networks. However, networks are very complex with many interactions, and have many unknown, unnoticed or unaccounted for vertices and/or edges. Changes in one vertices and/or edge of the network will ripple throughout the network and could affect large changes in other nodes of the network, which then feedbacks into the network causing more changes. Vertices may also have more or less importance (weight) on a network model (usually shown as a smaller or bigger dot), and the edges could have a stronger or weaker link (usually shown as a lighter or heavier line) on the network model. However, a minor change to either the vertices and/or edge of a less important vertices or edge can have a major impact on the network model. Statistical models may be inaccurate because they exist inside a network in a vertices or edge which may be unaccounted for in other vertices or edges.

\

A Network Topology

Dynamic science

Dynamic science Dynamic science always occurs when you have Chaos, Complexity, and Networks that have a change in conditions. When constants have been found to be inaccurate, or when the variables change, the science becomes dynamic. In addition, you must always consider Osborn’s Law that variables won’t; constants aren’t. Systems that are "complex" have distinct properties that arise from these relationships, such as nonlinearity, emergence, spontaneous order, adaptation, and feedback loops, among others. This dynamism is intrinsically very difficult to model with dynamic science due to the interdependencies and their relationships in the model or other types of interactions between the model parts, or between a given system and its external environment. As no system exists in a vacuum, any change to the external environment surrounding the system will change the model.

Examples of Chaos, Complexity, And Networks

To exemplify chaos, complexity, and networks I shall utilize a physical network and a social network.

Simple - Planetary Network

For a simple physical network consider the example of the Network of our Solar System and its Planets. Einstein’s General Theory of Relativity can accurately predict the revolutions of the Planets around the Sun. However, as the Planets interact gravitationally with each other as well as with the Sun these interactions need to be modeled. The Sun and the Planets would be the vertices of the Network. The Gravitational effect between the Planets, and between the Sun and the Planets would be the edges.

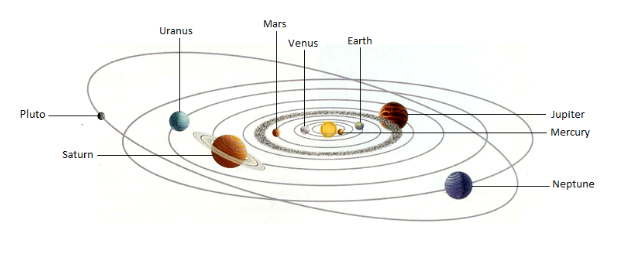
To accurately predict the orbits using Einstein’s General Relativity you need the precise masses, distances, and velocities between the Planets and the Sun. As the precise numbers are not known (and unknowable) the Network topology is imprecisely known. It needs to be noted that the orbit of an individual planet affects the orbits of the other planets (known as a perturbation in astronomy) which is integral to the Network topology. As the numbers that initiate the complex calculations to predict the orbits are imprecise the complexity issue increases within an individual planets orbit. This Complexity of an individual orbit affects the feedback into the Network edges (perturbations), which impacts the complexity of orbital calculations of the other vertices (Planets), which in turn impacts the other vertices and edges, ad infinitum. As this ad infinitum builds up Chaos is the result. Our predictions of planetary orbits are accurate for tens or hundreds of millions of years, but sometime in that timescale the orbital prediction will no longer be accurate due to Complexity, and then Chaos occurs.

The actual Planetary orbit can also change due to the unknown, unnoticed or unaccounted for factors (such as minor planets, asteroids, meteorites, and comets gravitational effects, or another unknown mass passes by our Solar System). The Planetary actual orbits will change due to the unknown, unnoticed or unaccounted factors. Thus, Network science, Chaos and Complexity is embodied in our Solar System in both a predictive and an actual manner.

Intermediate  – Internet Routing

The Internet was one of the first intermediate routing schemes to be developed. Prior to internet routing, land-line telecommunications were simple (in concept) switched networks operating in a linear fashion. Picking up a telephone handset opened a connection to the neighborhood relay station, which then opened a connection to another relay station, which then opened a connection to another relay station, and so on until a connection was established to the destination neighborhood relay station, which opened the connection to the destination telephone. After this linear connection was established, it remained in place until one party hung up their telephone or a disruption occurred, which required that another linear connection be established by one party or the other redialing the telephone number.

In the Internet routing scheme, data is sent across the Internet via IP packets (chunks of data) from the Web Server, which has both a source and destination IP address in the packet. These packets are then routed through the Internet utilizing routers along with their routing tables to send the packet to the proper destination Web Server. Packet transmissions are not linear, as each packet can be routed through different nodes in the network where they are recombined at the destination Web Server. If a packet is disrupted in transmission, then the destination Web Server requests a retransmission of the individual packet from the source Web Server. The connection between the source and destination Web Server and the User is often linear, and disruptions in the connection between the User and Web Server result in the User being disconnected from the internet.

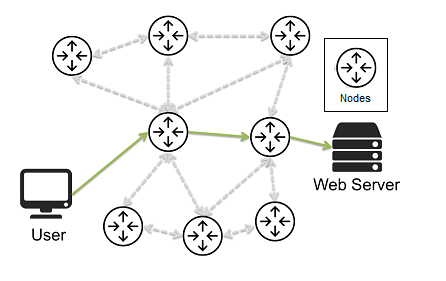
This transmission of the packets to and from the nodes of the network is more complex than, at first glance, it would appear. Too many nodes and the transmission of the data is delayed, while too few nodes increase the risk of disruptions. There are other factors, such as balancing the workload of the nodes and thus the network workload, as well as the availability of the nodes, must be accounted for to assure the speed and reliability of the network. These and other issues are where Network science is applied.

Complex – Cell Phone Routing

When we pick up our cell phone to place a call we do not recognize that this process utilizes a complex network to establish the connection. Consider the example of the diagram below.

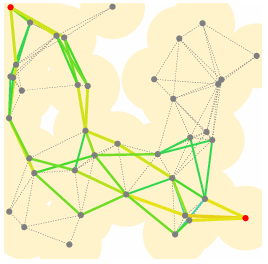
The cellphone (a vertice) on the upper left initiates the call to the cell phone (another vertice) on the lower right through the cell tower (a vertice) connection (an edge) to the other cell towers (vertices). There are many cell towers (vertices) and connections (edges) between the initiator and the receiver, and there are many paths that can be utilized to complete the connection. And sometimes there is no cell tower area in a line-of-sight (a dead zone). The connection path is constantly changing during your phone conversation due to many factors. The initiator or the receiver may be moving and moving to another cell tower area, which changes the route of the connection. In addition, a cell tower can become overloaded and it needs to transfer the connection to another cell tower to reduce its load. Perhaps the cell tower fails (electronics, electricity, weather, etc.), or is deliberately switched off for maintenance. Again, all of this will change the route of the connection. There is also the optimal path (the fewest cell towers needed to complete the connection) which is the most desirable path for both you (clarity and consistency of the call) and the cellphone company (the least amount of resources to make a connection). There are many other factors (too many to discuss in this article) that also affect the cellphone network. All these factors must be considered to provide for a more consistent and effective connection. A truly amazing feat of engineering, computer modeling, and computer control.

Chaos and complexity become involved in the predictions of the individual vertices, and the individual edges. You can computer model for each vertice and edge, but complexity happens within the model and the model predictions will sometimes not be the actual result. Chaos will eventually happen with the result of the failure of a vertice or edge, and perhaps the failure of the entire network (think of the large-scale electrical blackouts that have occurred in the past1).  Network science is utilized to plan for cell phone towers locations (vertices) and routing (edges), and to manage the vertices and edges when it is operational (in today's world this means 24/7/365). And all of this is done without human intervention and based on Network science and computer control.

1 The electrical distribution network is also an excellent example of a complex chaos, complexity, and network science.

Dynamic - Social Network

A Social Network social network is a social structure made up of a set of social actors (such as individuals or organizations), sets of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities as well as a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine network dynamics. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads and "web of group affiliations". Jacob Moreno is credited with developing the first sociograms in the 1930s to study interpersonal relationships. These approaches were mathematically formalized in the 1950s and theories and methods of social networks became pervasive in the social and behavioral sciences by the 1980s.  Social network analysis is now one of the major paradigms in contemporary sociology, and is also employed in a number of other social and formal sciences. Together with other complex networks, it forms part of the nascent field of network science The social network is a theoretical construct useful in the social sciences to study relationships between individuals, groups, organizations, or even entire societies (social units, see differentiation). The term is used to describe a social structure determined by such interactions. The ties through which any given social unit connects represent the convergence of the various social contacts of that unit. This theoretical approach is, necessarily, relational. An axiom of the social network approach to understanding social interaction is that social phenomena should be primarily conceived and investigated through the properties of relations between and within units, instead of the properties of these units themselves. Thus, one common criticism of social network theory is that individual agency is often ignored although this may not be the case in practice (see agent-based modeling). Precisely because many different types of relations, singular or in combination, form these network configurations, network analytics are useful to a broad range of research enterprises. In social science, these fields of study include, but are not limited to anthropology, biology, communication studies, economics, geography, information science, organizational studies, social psychology, sociology, and sociolinguistics.

In social networks when Economist, Statisticians, Politicians, Sociologist, Businessman and others who deal with human decisions by individuals or groups they need to be cognizant that there are many, many, factors that go into those individuals or groups decisions (the initial conditions). Some of these initial conditions may even be unknown, unnoticed or unaccounted for, including by both the individuals or groups making the decision and those attempting to model the system. And when circumstances change the decisions of individuals or groups will change. A change in the decisions of even a small group (or an individual) can propagate throughout the network and alter other individuals or groups in the network decision-making processes, which can then change the originators and other individual or group decisions within the network. This is known as network feedback, which changes the entire dynamic of the network.

Within the individuals or groups (vertices) there is also the initial conditions and the feedback that occurs within the vertices. Complexity states that if the minor initial starting values are not precisely known it can cause big differences in where things end up. Therefore, if your statistics are not precise (which they never are), and imprecise feedback is present, Complexity within the vertices increases. It is therefore impossible to predict a precise outcome which then leads to Chaos. Vertices changes are also transmitted through the network via the edges and the Network topology changes as a result, which changes the individual vertices in the network, which can also lead to Chaos. Chaos can cause large unexpected changes to occur in a system. In human interactions, these changes could be significant (such as an economic collapse or even a war).

Final Thoughts:

Chaos theory and Complex, Network, and Dynamic systems theory opens a breathtaking new perspective on the universe. All four of these theories can help us understand the universe in a way that can enrich our lives and help our understanding of how our societies, politics, economies, finance, commerce, and science/technologies interact and shape our world. We would all be better off and comprehend the forces that shape our world if we gained knowledge of these theories.

With the advent of high-speed computing and supercomputers, it is now possible to computer model chaos, complexity, and networks using Dynamic Systems Theory.. However, computer modeling as its own inherent issues, concerns, and limitations that can lead to incorrect results.  For more information on Computer Modeling, I would direct you to the article that I have written on this subject. Everyone needs to be aware of Chaos Theory, Complexity, Network, and Dynamics science when creating computer models and analyzing the results of the computer model, and especially their predictive models. Chaos Theory, Complexity, Network, and Dynamic science also reminds us that we live in a problemistic and not deterministic universe and, therefore, whenever anyone makes a prediction on the future the prediction cannot be definitive but only problematical. This is especially true when the computer model is dependent on human actions or human reactions to change. Humans are inherently unpredictable, thus, computer models that involve humans are not capable of being accurate.

Further Readings

For a brief introduction on these topics I would recommend the Oxford University Press series “A Very Short Introduction” on these subjects:

• Chaos: A Very Short Introduction, by Lenny Smith
• Complexity: A Very Short Introduction by John H. Holland
• Networks: A Very Short Introduction by Guido Caldarelli

Some interesting website with general scientific topics are:

• Ask a Mathematician / Ask a Physicist
• Ask the Physicist!
• Physics and Astronomy Ask the Experts
• The Skeptic's Dictionary
• Understanding Science – how science really works

Disclaimer

Please Note - many academics, scientist and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists, and engineers entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. I believe it is essential for all laypersons to grasp the concepts of this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.

Most academics, scientist, and engineers when speaking or writing for the general public (and many science writers as well) strive to be understandable to the general public. However, they often fall short on the understandability because of their commitment to accuracy and thoroughness, as well as some audience awareness factors. Their two biggest problems are accuracy and the audience knowledge of the topic.

Accuracy is a problem because academics, scientist, engineers and science writers are loath to be inaccurate. This is because they want the audience to obtain the correct information, and the possible negative repercussions amongst their colleagues and the scientific community at large if they are inaccurate. However, because modern science is complex this accuracy can, and often, leads to confusion amongst the audience.

The audience knowledge of the topic is important as most modern science is complex, with its own words, terminology, and basic concepts the audience is unfamiliar with, or they misinterpret. The audience becomes confused (even while smiling and lauding the academics, scientists, engineers or science writer), and the audience does not achieve understandability. Many times, the academics, scientists, engineers or science writer utilizes the scientific disciplines own words, terminology, and basic concepts without realizing the audience misinterpretations, or has no comprehension of these items.

It is for this reason that I place understandability as the highest priority in my writing, and I am willing to sacrifice accuracy and thoroughness to achieve understandability. There are many books, websites, and videos available that are more accurate and through. The subchapter on “Further Readings” also contains books on various subjects that can provide more accurate and thorough information. I leave it to the reader to decide if they want more accurate or through information and to seek out these books, websites, and videos for this information.