The Personal Website of Mark W. Dawson

Containing His
Articles, Observations, Thoughts, Meanderings,
and some would say Wisdom (and some would say not).
Computer Modeling
- Introduction
- Computer Modeling
- Chaos, Complexity, and Network Science
- GIGO – Garbage In Garbage Out
- Open and Closed Systems
- Computer Modeling is a Tool
- Final Thoughts
- Further Readings
- Disclaimer
Introduction
This article is an examination of the issues, concerns, and limitations when utilizing Computer Models in science, engineering, and public policy formulation. I will not delve into specific details of Computer Modeling, nor will I be utilizing any sciences or mathematics in examining the issues, concerns, and limitations of computer modeling.
I should point out that I am NOT a scientist or engineer, nor have I received any education or training in science or engineering. This paper is the result of my readings on this subject in the past decades. Many academics, scientists, and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists and engineers’ entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. When writing for the general public this accuracy and thoroughness can often lead to less understandability. I believe it is essential for all laypersons to grasp the concepts of within this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.
Computer Modeling
With the advent of electronic computing new software tools were developed to assist scientists with predictions and engineers with their designs. Scientific software tools are known as Computer Simulations and the simulation computer programs are usually developed with specific purpose computer programs. Engineering software tools generally fall into three categories; Computer Aided Design (CAD), Computer Aided Engineering (CAE), and Computer Aided Manufacturing (CAM), which are usually created with general purpose computer engineering modeling software programs.
Computer Simulation
Computer Simulation of scientific systems is generally utilized for predictions. The scientist wants to understand how a system works, and what changes to the system will occur if you change a circumstance within the system (initial values, feedback, external stimuli, etc.).
Computer simulations are computer programs that can be either small, running almost instantly on small devices, or large-scale programs that run for hours or days on network-based groups of computers. The scale of events being simulated by computer simulations has far exceeded anything possible (or perhaps even imaginable) using traditional paper-and-pencil mathematical modeling. Over 10 years ago, a desert-battle simulation of one force invading another involved the modeling of 66,239 tanks, trucks and other vehicles on simulated terrain around Kuwait, using multiple supercomputers in the DoD High Performance Computer Modernization Program. Other examples include a 1-billion-atom model of material deformation; a 2.64-million-atom model of the complex protein-producing organelle of all living organisms, the ribosome, in 2005; a complete simulation of the life cycle of Mycoplasma genitalium in 2012; and the Blue Brain project at EPFL (Switzerland), begun in May 2005 to create the first computer simulation of the entire human brain, right down to the molecular level. |
Computer-aided Design (CAD)
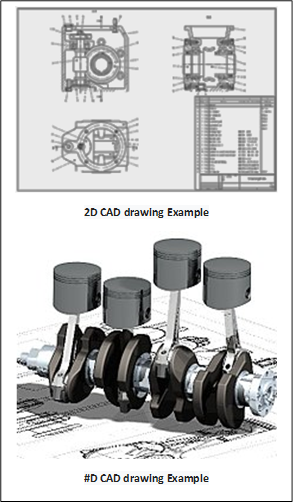 |
Computer-aided design (CAD) is the
use of computer systems (or workstations) to aid in the
creation, modification, analysis, or optimization of an
engineering design. CAD software is used to increase the
productivity of the designer, improve the quality of design,
improve communications through documentation, and to create
a database for manufacturing. CAD output is often in the
form of electronic files for print, machining, or other
manufacturing operations. The term CADD (for Computer Aided
Design and Drafting) is also used. Its use in designing
electronic systems is known as Electronic Design Automation
(EDA). In mechanical design it is known as Mechanical Design
Automation (MDA) or Computer-Aided Drafting (CAD), which
includes the process of creating a technical drawing with
the use of computer software.
CAD is an important industrial art extensively used in many applications, including automotive, shipbuilding, and aerospace industries, industrial and architectural design (building information modeling), prosthetics, and many more. CAD is also widely used to produce computer animation for special effects in movies, advertising and technical manuals, often called DCC digital content creation. The modern ubiquity and power of computers means that even perfume bottles and shampoo dispensers are designed using techniques unheard of by engineers of the 1960s. Because of its enormous economic importance, CAD has been a major driving force for research in computational geometry, computer graphics (both hardware and software), and discrete differential geometry. |
Computer-aided Engineering (CAE)
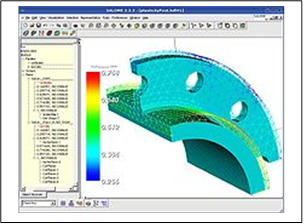 |
Computer-aided engineering (CAE) is
the broad usage of computer software to aid in engineering
analysis tasks. It includes finite element analysis (FEA),
computational fluid dynamics (CFD), multibody dynamics
(MBD), and optimization. Software used to analyse CAD
geometry tools that have been developed to support these
activities are considered CAE tools. CAE tools are being
used, for example, to analyze the robustness and performance
of components and assemblies. The term encompasses
simulation, validation, and optimization of products and
manufacturing tools. In the future, CAE systems will be
major providers of information to help support design teams
in decision making. Computer-aided engineering is used in
many fields such as automotive, aviation, space, and
shipbuilding industries.
In regard to information networks, CAE systems are individually considered a single node on a total information network and each node may interact with other nodes on the network. CAE systems can provide support to businesses. This is achieved by the use of reference architectures and their ability to place information views on the business process. Reference architecture is the basis from which information model, especially product and manufacturing models. |
Computer Aided Manufacturing (CAM)
 |
Computer Aided Manufacturing (CAM) is the use of software
to control machine tools and related ones in the
manufacturing of workpieces. This is not the only definition
for CAM, but it is the most common; CAM may also refer to
the use of a computer to assist in all operations of a
manufacturing plant, including planning, management,
transportation and storage. Its primary purpose is to create
a faster production process and components and tooling with
more precise dimensions and material consistency, which in
some cases, uses only the required amount of raw material
(thus minimizing waste), while simultaneously reducing
energy consumption.[citation needed] CAM is now a system
used in schools and lower educational purposes. CAM is a
subsequent computer-aided process after computer-aided
design (CAD) and sometimes computer-aided engineering (CAE),
as the model generated in CAD and verified in CAE can be
input into CAM software, which then controls the machine
tool. CAM is used in many schools alongside Computer-Aided
Design (CAD) to create objects.
Computer Aided Manufacturing (CAM) is the use of software to control machine tools and related ones in the manufacturing of workpieces. This is not the only definition for CAM, but it is the most common; CAM may also refer to the use of a computer to assist in all operations of a manufacturing plant, including planning, management, transportation and storage. Its primary purpose is to create a faster production process and components and tooling with more precise dimensions and material consistency, which in some cases, uses only the required amount of raw material (thus minimizing waste), while simultaneously reducing energy consumption.[citation needed] CAM is now a system used in schools and lower educational purposes. CAM is a subsequent computer-aided process after computer-aided design (CAD) and sometimes computer-aided engineering (CAE), as the model generated in CAD and verified in CAE can be input into CAM software, which then controls the machine tool. CAM is used in many schools alongside Computer-Aided Design (CAD) to create objects. |
The issues that I will examine is that of the limitations of computer modeling. Most people are aware of what computer modeling is, but they have little understanding of how difficult it can be, and the limitations of computer modeling.
The Limits of Human Knowledge
The first thing to keep in mind when dealing with any scientific or engineering subject is that it is very important to remember three things about the limitations of human knowledge:
- That we know what we know, and we need to be sure that what we know is correct.
- That we know what we don't know, and that allowances are made for what we don’t know.
- That we don't know that we don't know, which cannot be allowed for as it is totally unknown.
The limits of human knowledge are expanding, but there is much more that we don’t know then there is what we do know. Indeed, even when we know what we know, what we know may be incorrect. What we know that that we don’t know always leads to ambiguity, mistakes and false conclusions. That which we don't know that we don't know is the killer in any scientific or engineering endeavor. Always be cognizant of these three items when dealing with any scientific or engineering subject.
Chaos, Complexity, and Network Science
What are chaos, complexity, and network science, and what does it have to do with this subject. Directly Everything and Indirectly Everything! If you are going to create, develop or utilize scientific and engineering studies you need to be aware of chaos, complexity, and network science. You first need to understand something of chaos, complexity and network science to understand their impact on this subject. For this understanding, I have prepared another article “Chaos, Complexity, and Network Science” that I would direct you too. Briefly, however, Chaos, Complexity, and Networks Science is as follows:
Chaos theory is the field of study in mathematics and science that studies the behavior and condition of dynamical systems that are highly sensitive to initial conditions, a response popularly referred to as the butterfly effect (Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?). Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.
Complexity characterizes the behavior of a system or model whose components interact in multiple ways and follow local rules, meaning there are no reasonable means to define all the various possible interactions. Complexity arises because some systems are very sensitive to their starting conditions so that a tiny difference in their initial starting conditions can cause big differences in where they end up. And many systems have a feedback into themselves that affects their own behavior, which leads to more complexity.
Network science studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks. Distinct elements or actors represented by nodes, and the links between the nodes, define the network topology. A change in a node or link is propagated throughout the network and the Network Topology changes accordingly. Network science draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology.
GIGO – Garbage In Garbage Out
At the dawn of the computer age there was an acronym that was frequently used; GIGO – Garbage In -> Garbage Out. It referred to the situation that if your inputs were incorrect your outputs would be incorrect. It left unspoken that if your processing instructions (computer program) were incorrect anything in would produce incorrect outputs. The correct acronym should have been GIGPGO (Garbage In -> Garbage Processing -> Garbage Out), not pronounceable, and an admittance that computer programs contained mistakes. As computer programs became more complex GIGPGO became more pronounced. Today’s computer programming is very complex, and the most complex programming is computer modeling. In computer modeling, the number of formulas (algorithm’s) and the number of interrelationships between the algorithms are so complex that rarely is a computer model that is written is done by one person. Many computer models are produced by general computer modeling programming toolkits, which themselves are very complex. Computer modeling and computer modeling toolkits are usually written by a team of very knowledgeable and very experienced computer programmers. But team programming is fraught with problems, as team members are human, and humans make mistakes and miscommunicate, the results of which are imperfect computer modeling program. Many team computer programming efforts have extensive procedures, policies, and testing to reduce these potential mistakes, but mistakes will happen. In addition, the computer programmers are rarely Subject Matter Experts, and Subject Matter Experts are rarely (excellent) computer programmers. Therefore, GIGPGO is always present, and indeed it has been stated that all computer models are incorrect - but many are useful. GIGPGO must always be kept in mind when examining the results of a computer model as all computer modeling contain GIGPGO.
It should also be noted that fixing an error in a computer model may be easy or difficult. Fixing the consequence of utilizing an incorrect computer model is usually difficult, and the consequences can often lead to a disaster. Many of today’s computer models are reliable but imperfect. When mistakes are uncovered they are corrected and learned from (every problem is a learning experience). The accumulation of learning experiences leads to better and more reliable computer models, but many more learning experiences are to be expected, and many improvements to computer modeling software will have to be undertaken.
Open and Closed Systems
Computer modeling has at its core three levels of difficulty ' Simple Modeling, Complex Modeling, and Dynamic Modeling. This is usually based on whether the computer model is of an open or closed system.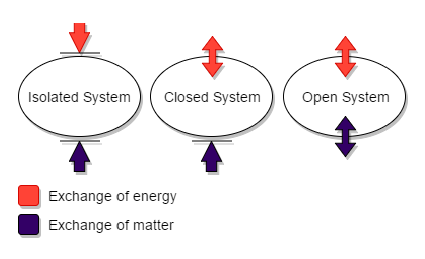
Isolated, Open, and Closed Systems
In physical science, an Isolated System is either of the following:
- a physical system so far removed from other systems that it does not interact with them.
- a thermodynamic system enclosed by rigid immovable walls through which neither mass nor energy can pass.
A Closed System is a physical system that does not allow certain types of transfers (such as transfer of mass and energy transfer) in or out of the system. The specification of what types of transfers are excluded varies in the closed systems of physics, chemistry or engineering.
An Open System is a system that has external interactions. Such interactions can take the form of information, energy, or material transfers into or out of the system boundary, depending on the discipline which defines the concept. An open system is contrasted with the concept of an isolated system which exchanges neither energy, matter, nor information with its environment. An open system is also known as a constant volume system or a flow system.
The concept of an open system was formalized within a framework that enabled one to interrelate the theory of the organism, thermodynamics, and evolutionary theory. This concept was expanded upon with the advent of information theory and subsequently systems theory. Today the concept has its applications in the natural and social sciences.
In the natural sciences, an open system is one whose border is permeable to both energy and mass. In thermodynamics, a closed system, by contrast, is permeable to energy but not to matter.
Open systems have a number of consequences. A closed system contains limited energies. The definition of an open system assumes that there are supplies of energy that cannot be depleted; in practice, this energy is supplied from some source in the surrounding environment, which can be treated as infinite for the purposes of the study. One type of open system is the radiant energy system, which receives its energy from solar radiation ' an energy source that can be regarded as inexhaustible for all practical purposes.
Closed Systems are easier and more accurate to computer model but are less reliable in the real-world (an open system). Open Systems are much more difficult to computer model and are less accurate of the real-world as the inputs and outputs to the closed system are numerous, imprecise, and variable. Dynamic computer models tend to be of Open Systems, while simple computer models are usually of a closed system. Complex computer models tend to have subsystems of closed computer models while the entire system can be an open system or closed system.Computer Modeling is a Tool
Computer modeling is done by both scientists and engineers and is a very powerful tool for both scientists and engineers, but it is only a TOOL – not an ANSWER. The tool itself may contain errors that produce a wrong answer. Additionally, the tool may work well in the conceptional design but not so well in the reality.
The base problem with computer modeling is twofold; 1) verification, validation, and confirmation, and 2) correlation vs. causation. Verification and validation of numerical models of natural systems is impossible. This is because natural systems are never closed and because model results are always nonunique. Models can be confirmed by the demonstration of agreement between observation and prediction, but confirmation is inherently partial. Complete confirmation is logically precluded by the fallacy of affirming the consequent and by incomplete access to natural phenomena. Models can only be evaluated in relative terms, and their predictive value is always open to question. The primary value of models is heuristic. A heuristic technique, often called simply a heuristic, is an approach to problem-solving, learning, or discovery that employs a practical method not guaranteed to be optimal or perfect, but sufficient for the immediate goals. A good outline of this problem is “Verification, Validation, and Confirmation of Numerical Models in the Earth Science” (from which this paragraph was extracted). The other issue of correlation vs. causation is how can you know that the results of your computer model are reflecting the actual cause (causation), or are they merely appearing to be the cause (correlation). To determine this, you need to mathematically prove that your computer model is scientifically correct, which may be impossible. What most computer models undergo is an iterative process of refinement to obtain the best possible model as diagramed below:
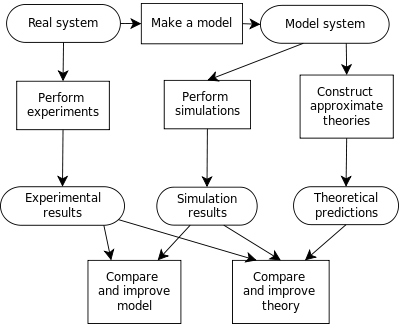
Even with this process your computer model will be incomplete or incorrect. This is because the computer model is created by humans, and humans make mistakes no matter how careful they are, or how many humans are involved in the creation or validation of the model. The information that goes into the computer model may also be incorrect, or the interactions between the components may not be known or knowable. And there may simply be too many real-world constants or variables to be computer modeled. As a result, the computer model will not completely reflect the actual problem it is modeling. Therefore:
Computer modeling is only a tool for science and engineering – not a proof of the science or engineering.
You should also remember:
Computer Models are great tools for helping you think,… just never rely on them to do the thinking for you.
Computer modeling has at its core three levels of difficulty – Simple Modeling, Complex Modeling, and Dynamic Modeling. Some examples regarding computer models are as follows. Please remember that these examples only deal with the most general aspects of the problems. The details are even more complex. And as always, the devil is in the details. The following are some examples of Simple Modeling, Complex Modeling, and Dynamic Modeling in Engineering and Scientific Computer Modeling.
Systems Engineering
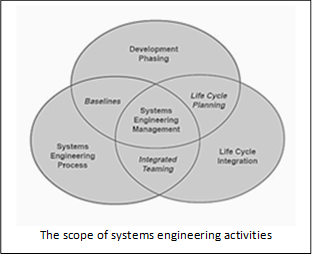
Systems engineering is an interdisciplinary field of engineering and engineering management that focuses on how to design and manage complex systems over their life cycles. At its core, systems engineering utilizes systems thinking principles to organize this body of knowledge. Issues such as requirements engineering, reliability, logistics, coordination of different teams, testing and evaluation, maintainability and many other disciplines necessary for successful system development, design, implementation, and ultimate decommission become more difficult when dealing with large or complex projects. Systems engineering deals with work-processes, optimization methods, and risk management tools in such projects. It overlaps technical and human-centered disciplines such as industrial engineering, mechanical engineering, manufacturing engineering, control engineering, software engineering, electrical engineering, cybernetics, organizational studies and project management. Systems engineering ensures that all likely aspects of a project or system are considered, and integrated into a whole. The systems engineering process is a discovery process that is quite unlike a manufacturing process. A manufacturing process is focused on repetitive activities that achieve high quality outputs with minimum cost and time. The systems engineering process must begin by discovering the real problems that need to be resolved, and identify the most probable or highest impact failures that can occur – systems engineering involves finding solutions to these problems. |
Systems Engineering techniques are often utilized in the development of Computer Engineering Models. This is done to help assure that the computer model reflects the real-world environment that the computer model was developed for. It also, potentially, helps reduce the errors that can occur within computer models and make them more accurate. Good Systems Engineering can lead to better computer models, but it will not eliminate the issues, concerns, and limitations of computer modeling.
Computer Modeling Systems Examples
Engineering Modeling Systems
Engineering Simple Modeling
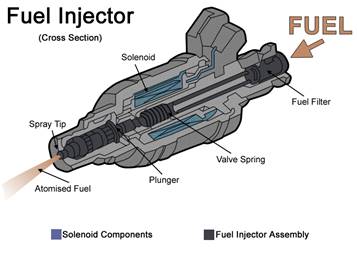
Simple modeling is when you are working on a small subsystem that has a limited function, and few (hundreds or maybe a thousand) of constants and variables in its engineering. An example would be the development of new gasoline fuel injector for an automobile.
A gasoline fuel injector, at its core, is a pump (with a piston) that is attached to the fuel injector. The fuel injector in its basic form is a hollow cylinder that becomes a hollow cone (or conic), with the cone having a spray tip. There are various other components of a fuel injector that may be ignored for the purposes of this article. There are many problems and issues when designing this fuel injector – mainly in the flow of the gasoline through the system. This flow is based on the science of fluid dynamics which is a very complex science. When designing a fuel injector you must consider that all parts are working optimally. In the computer model the pressure from the pump on the gasoline is consistent, the flow through the cylinder is constant and uniform, and the cone channels the gasoline through the fuel injector uniformly. However, this is rarely the case in a real-world fuel injector. The pump has minor variations in its pressure, and the pressure may not be consistent over the entire area of entry. The cylinder is assumed to be uniformly circular in its circumference, but minor variations of circumference occur during the manufacturing of the cylinder, as well as small pits and burs on the surface of the cylinder which will interfere with the flow of the gasoline. The cone has the same issues as the cylinder, was well as the spray tip having minor variations during the manufacturing. Additionally, the seals between these components may not be perfect or uniform and could interfere with the flow of the gasoline. The gasoline itself is assumed to be pure, but in the real-world gasoline has many particles and particulates mixed within. And of course, the fuel injector operates in a stressful environment (mainly vibrations and temperature).
Good engineering design allows for these issues, and they try to model for these variations in both the individual elements as well as the system as a whole. But it is not possible to know all the possibilities, nor all the conditions in which the fuel injector will operate. Therefore, the fuel injector design will not match the real-world, which is why engineers build an actual fuel injector and do extensive tests on the actual fuel injector before putting it into production. The following diagram is a simple cutaway of a fuel injector.
Engineering Complex Modeling
Complex modeling occurs when you incorporate all the simple models (subsystems) together to form the whole system. Not only must the subsystems be working properly, but the interactions between the subsystems (and interactions between multiple subsystems) function properly. A good example of this is in the design of an automobile.
Automobiles have hundreds of subsystems (such as engine, transmission, axles, tires, brakes, frame, steering, bumpers and crash control, lighting and signals, bodies, etc.). Today’s automobiles also have computer controls of these subsystems, which adds another layer of complexity. These subsystems must work together and properly within the computer model before a mock-up test vehicle is created. You must also account for the conditions under which the automobile operates, such as – startup, acceleration/deceleration, braking, steering, road surface, weather and temperatures, and altitude, etc... Many of these factors are well known and can be modeled to a degree of accuracy – but not all are known. This is indeed a complex task. The following diagram give you an idea of the subsystems that go into an automobile design.

Engineering Dynamic Modeling
Dynamic modeling occurs when you have subsystems of complex modeling working together, or when external factors are complex and varying. An example of this is modern aircraft manufacturing. For simple aircraft, such as private aircraft, a complex model will often suffice. But when you are designing a commercial aircraft you must have a dynamic model. Some of these issues are:
A commercial aircraft has hundreds (if not thousands) of complex modeling systems working together. Consider the following diagram of an Airbus A380 aircraft that lists the major subsystems of the aircraft.
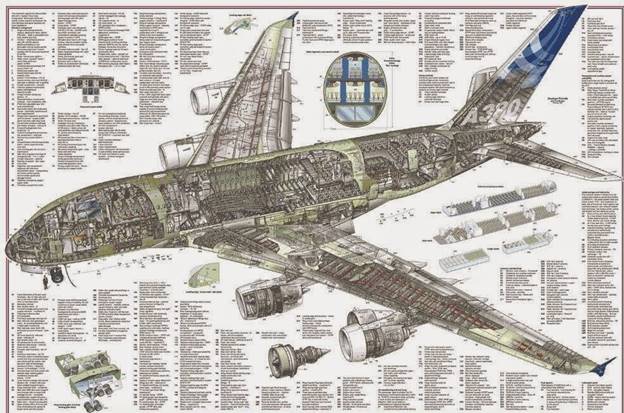
As you can imagine the dynamic computer modeling for all these interactions between these complex computer models is very difficult. Changes in one complex computer model have impacts on the other complex computer models. And the computer modeling of the aircraft systems and subsystems is not all that is required. You must computer model the environment in which the aircraft operates. Taxiing, takeoff and landings, cruising, weather, temperature, turbulence, and air pressure, etc. are some of the items to be computer modeled. Changes in atmospheric conditions during flight and their impact on the aircraft when all these changes are occurring must also be computer modeled. And these environmental changes have feedback to the aircraft's systems performance. This is what makes it a dynamic computer model. Not to mention the possibility of human error of the pilots, flight crews, and ground crews that may lead to failure. It is not possible to know all the conditions that may be encountered by an aircraft, so failure occurs as a result of unknown or unexpected conditions.
Scientific Modeling Systems
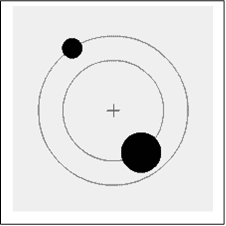
Computer Model - Simple - Planetary Orbits
|
For a simple scientific model consider the example of the orbits of the planets in our solar system. As the planets interact gravitationally with each other as well as with the sun these interactions can be computer modeled. Newton’s Universal Gravity can be utilized to predict the planetary orbits, but as a theory is incorrect so will the predictions be incorrect. However, Newton’s mathematics is complex but easy to computer model. Einstein’s General Theory of Relativity can accurately predict the revolutions of the planets around the Sun, but the mathematics is very complex and therefore the computer modeling is complex.
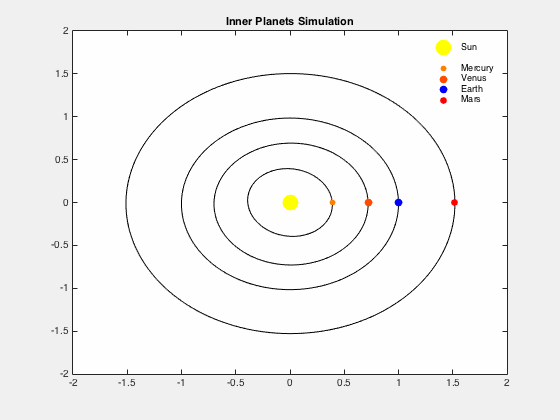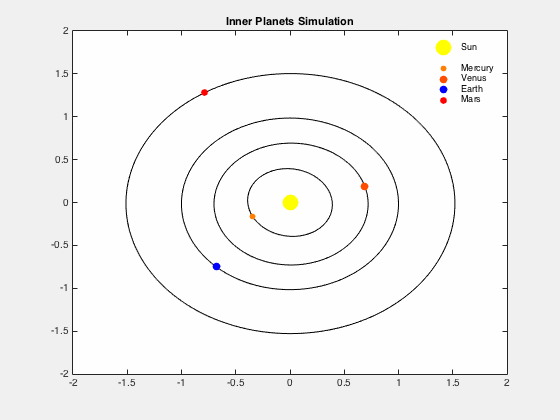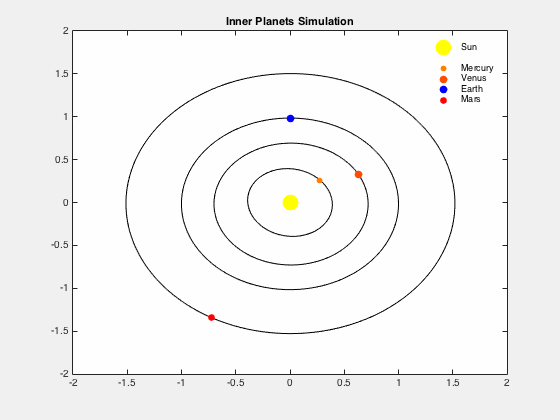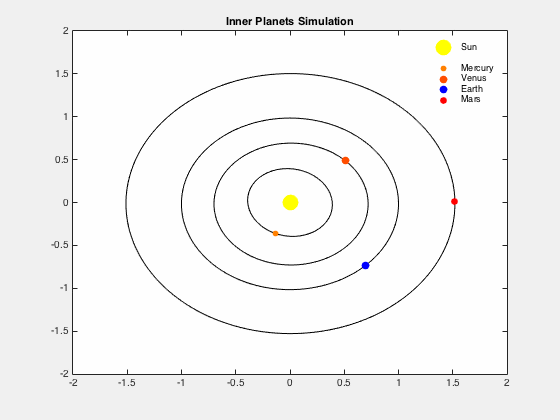
To accurately predict the orbits using Einstein’s General Relativity you need the precise masses, distances, and velocities between the planets and the Sun. As the precise numbers are not known and unknowable the computer model will be imprecise.
It should also be noted that the orbit of an individual Planet affects the orbits of the other planets (known as perturbations in astronomy) which is integral to the computer modeling. The actual planetary orbit can also change due to the unknown, unnoticed or unaccounted for factors such as minor planets, asteroids, meteorites, and comets gravitational effects, or other unknown masses passing by our solar system. The planetary actual orbits will change due to these unknown, unnoticed or unaccounted for factors.
The newer scientific branch of Chaos, Complexity, and Network Science also play a factor in all scientific modeling systems. The subject of Chaos, Complexity, and Network Science, and its issues and concerns is another paper that I have written that is beyond the scope of this paper. I would direct you to this paper for further information on this subject.
Therefore, the planetary orbits computer model is only an approximation, but useful enough for scientific purposes.
Computer Model - Complex – Fluid Dynamics
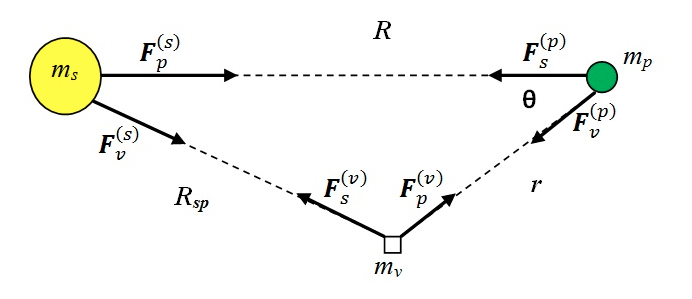
For a complex Scientific Computer Model, we must consider the example of the Science of fluid dynamics. The branch of the science of fluid mechanics is concerned with the movement of gases and liquids. In a simple closed system with no external factors, fluid dynamics is complex to computer model. When external factors are introduced this leads to very complex computer modeling.
|
The size of the containment cylinder, the density and volume of the two fluids, and the force of the lighter fluid on the heavier fluid are variables that can change the results of the computer model. Changing any one of these variables will change the computer model. Changing more than one variable has an even larger effect on the computer model.
When this model is running an open system (such as the Earth’s atmosphere) its subjects the computer model to outside forces (such as wind, barometric pressure changes, interference from other nearby masses, etc.) and makes the computer model much more complex and therefore more unreliable.
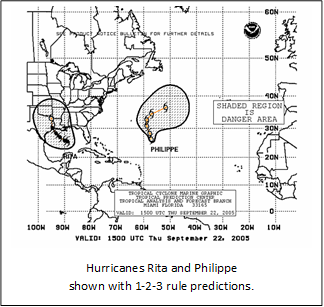
Computer Model - Dynamic – Hurricane Forecasting
|
How often have we watched a weather forecast of a hurricane, and how often has the forecast been confusing or even wrong. Unfortunately, much too often. This is because hurricane forecasting, and weather forecasting, is a dynamic computer model. There are many constants and variables that go into a hurricane computer model forecast, and these constants and variables are not precisely known. There are also internal and external factors that feedback on to each other that change the dynamics of the computer model.
Not only do we have the dynamics of what is happening in the actual hurricane, but we have the dynamics of the atmosphere surrounding the hurricane, the dynamics of the oceans below, and the dynamics of the land mass the hurricane encounters. All these dynamics must be accounted for in Hurricane forecasting. This is why hurricane forecasting will generally show three possible paths of a hurricane, and even these three paths can be wrong, as the following real-world example demonstrates:
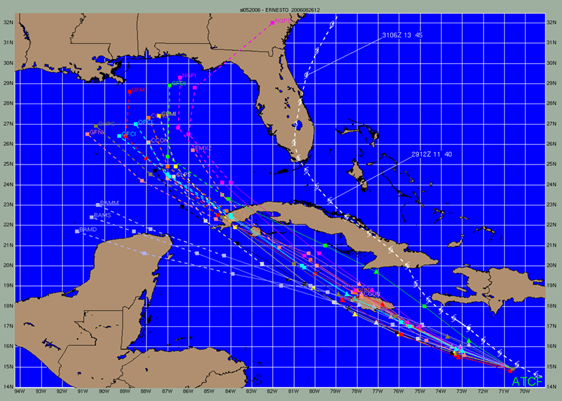
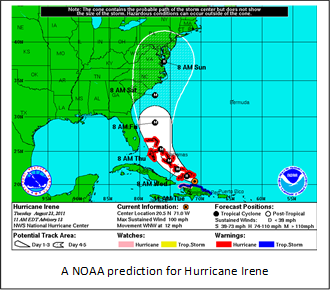
The NHC official forecast for Ernesto (2006) is light blue, while the storm's actual track is the white line over Florida.
As can be seen from this example the real-world track bore no relation to the computer model. This was because of imprecise constants and variables of the hurricane, as well as the dynamics of all the factors that contributed to the real world and computer model disparities. As more, and better information was obtained by the NHC they revised their forecast (as shown in the Wikipedia tropical Cyclone forecast model image) but even this forecast was incorrect for the real-world path.
The lesson to be learned from this is dynamic computer modeling is imprecise and often inaccurate due to the before mention factors. You should always keep this in mind when dealing with dynamic computer models and be aware that the model is probably wrong – but it may be useful.
Final Thoughts
Most scientific and engineering endeavors utilize Computer Modeling. Therefore, you need to know the issues, concerns, and limitations of Computer Modeling to determine its impact on the scientific and engineering endeavors.
Computer modeling has at its core three levels of difficulty – Simple Modeling, Complex Modeling, and Dynamic Modeling. Simple modeling is when you are working on a model that has a limited function; a few (hundreds or maybe a thousand) of constants and variables within the components of the model, and a dozen or so interactions between the components of the model. Complex modeling occurs when you incorporate many simple models (subsystems) together to form a whole system, or where there are complex interactions and/or feedback within and between the components of the computer model. Not only must the subsystems be working properly, but the interactions between the subsystems must be modeled properly. Dynamic modeling occurs when you have subsystems of complex modeling working together, or when external factors that are complex and varying are incorporated into the computer model.
The base problem with computer modeling is twofold; 1) verification, validation, and confirmation, and 2) correlation vs. causation. Verification and validation of numerical models of natural systems are impossible. This is because natural systems are never closed and because model results are always nonunique. The other issue of correlation vs. causation is how can you know that the results of your computer model are reflecting the actual cause (causation), or are they merely appearing to be the cause (correlation). To determine this, you need to mathematically prove that your computer model is scientifically correct, which may be impossible. You should also remember the following:
"All models are wrong, some are useful." - George E. P. Box, one of the great statistical minds of the 20th century
The first thing to keep in mind when dealing with computer models is that when thinking about a computer model it is very important to remember three things:
- That we know what we know, and we need to be sure that what we know is correct.
- That we know what we don't know, and that allowances are made for what we don’t know.
- That we don't know that we don't know, which cannot be allowed for as it is totally unknown.
It is numbers 2 and 3 that often is the killer in computer modeling and often leads to incorrect computer models.
You also need to keep in mind the other factors when utilizing computer models:
- Constants and Variables within a component of the computer model are often imprecisely known leading to incorrect results within the components, which then get propagated throughout the computer model.
- The interactions between the components are often not fully understood and allowed for, and therefore not computer modeled correctly.
- The feedback and/or dynamics within the computer model is imprecise, or not fully known, which leads to an incorrect computer model.
All these factors will result in the computer model being wrong. And as always remember GIGPGO (Garbage In -> Garbage Processing -> Garbage Out).
You should also be aware that when computer modeling is utilized to model for a long period of time the longer the time period modeled the more inaccurate the computer model will become. This is because the dynamics and feedback errors within the computer model build up which affects the long-term accuracy of the computer model. Therefore, long-term predictions of a computer model are highly suspect. Another thing to be aware of is that if you are computer modeling for a shorter period of time it needs to be of a sufficient period of time to determine the full effects of the computer model or to provide results that are truly useful. Too short of a time period will provide inconclusive (or wrong) results to be practicable. Therefore, short-term predictions of a computer model can be suspect.
And finally, Chaos, Complexity, Network, and Dynamic Science have an impact on computer models that cannot be properly accounted for, which affects the accuracy of the computer model. With the advent of high-speed computing and supercomputers, it is now possible to computer model chaos, complexity, and networks using Dynamic Systems Theory. Everyone needs to be aware of Chaos Theory, Complexity, Network, and Dynamics science when creating computer models and analyzing the results of the computer model, and especially their predictive models. Chaos Theory, Complexity, Network, and Dynamic science also reminds us that we live in a problemistic and not deterministic universe and, therefore, whenever anyone makes a prediction on the future the prediction cannot be definitive but only problematical. This is especially true when the computer model is dependent on human actions or human reactions to change. Humans are inherently unpredictable, thus, computer models that involve humans are not capable of being accurate.
The lesson from this paper is that a computer model is not an answer but a tool – and don’t trust the computer model but utilize the computer model. The computer modeling system itself may contain errors in its programming. The information that goes into the computer model may be incorrect, or the interactions between the components may not be known or knowable. And there may simply be too many real-world constants and variables to be computer modeled. Use the computer model as a tool and not an answer, and above all use your common sense when evaluating the computer model. If something in the computer model is suspicious examine it until you understand what is happening.
Further Readings
Unfortunately, as the field of Computer Modeling has become very specialized and complex there is only one book that I have found that provided the basic concepts for the general public:
The Promise and Limits of Computer Modeling by Charles Blilie
I would also direct you to the following websites that have discussions on the issues and concerns with Computer Modeling.
- A Model World
- A Skeptic's Guide to Computer Models
- Advantages and Disadvantages of Simulation
- Computer Simulations in Science
- Issues Regarding Computer Modeling and Simulation
- Science relies on computer modeling – so what happens when it goes wrong?
Some interesting website with general scientific topics are:
- Ask a Mathematician / Ask a Physicist
- Ask the Physicist!
- Physics and Astronomy Ask the Experts
- The Skeptic's Dictionary
- Understanding Science – how science really works
Disclaimer
Please Note - many academics, scientist and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists, and engineers entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. I believe it is essential for all laypersons to grasp the concepts of this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.
Most academics, scientist, and engineers when speaking or writing for the general public (and many science writers as well) strive to be understandable to the general public. However, they often fall short on the understandability because of their commitment to accuracy and thoroughness, as well as some audience awareness factors. Their two biggest problems are accuracy and the audience knowledge of the topic.
Accuracy is a problem because academics, scientist, engineers and science writers are loath to be inaccurate. This is because they want the audience to obtain the correct information, and the possible negative repercussions amongst their colleagues and the scientific community at large if they are inaccurate. However, because modern science is complex this accuracy can, and often, leads to confusion amongst the audience.
The audience knowledge of the topic is important as most modern science is complex, with its own words, terminology, and basic concepts the audience is unfamiliar with, or they misinterpret. The audience becomes confused (even while smiling and lauding the academics, scientists, engineers or science writer), and the audience does not achieve understandability. Many times, the academics, scientists, engineers or science writer utilizes the scientific disciplines own words, terminology, and basic concepts without realizing the audience misinterpretations, or has no comprehension of these items.
It is for this reason that I place understandability as the highest priority in my writing, and I am willing to sacrifice accuracy and thoroughness to achieve understandability. There are many books, websites, and videos available that are more accurate and through. The subchapter on “Further Readings” also contains books on various subjects that can provide more accurate and thorough information. I leave it to the reader to decide if they want more accurate or through information and to seek out these books, websites, and videos for this information.
If you have any comments, concerns, critiques, or suggestions I can be reached at mwd@profitpages.com.
I will review reasoned and intellectual correspondence, and it is possible that I can change my mind,
or at least update the content of this article.