The Personal Website of Mark W. Dawson

Containing His
Articles, Observations, Thoughts, Meanderings,
and some would say Wisdom (and some would say not).
The Universality of Gravity
- Containing His Articles, Observations, Thoughts, Meanderings, and some would say Wisdom (and some would say not).
- The Universality of Gravity
- Introduction
- The Ages of Physics
- Background
- The Motion of the Sun, Moon, and Planets
- Aristotle
- Other Greeks
- Claudius Ptolemy
- Nicolaus Copernicus
- Tycho Brahe
- Johannes Kepler
- Galileo Galilei
- Isaac Newton
- James Clerk Maxwell
- Albert Einstein
- An Outline of Einstein’s Life
- The Equivalence Principle
- Geometric Mathematics
- Einstein’s Character
- Some of the Consequences of General Relativity
- Additional Thoughts
- Final Thoughts
- Further Readings
- Timeline of Gravitational Physics and General Relativity
- Disclaimer
Introduction
This paper is an overview of the development of Gravitational Physics. It is done by focusing on ten scientists who were crucial in its development. Although thousands of scientists have contributed to the development of Gravitational Physics the ten scientists presented here have made such a significant impact as to change the course of Gravitational Physics. It is, therefore, a biographical history of Gravitational Physics. The scientific information is presented in general terms, and there is no mathematics. For those wishing more scientific details and/or mathematics, I have included a “Further Readings” section of books I would recommend that have more details and are readable by the general public.
Gravity is the only universal force, as that it exists in all places and at all times (space-time). Whereas the other forces exist only in their local area of space-time. Gravity is also the weakest of all forces, by many orders of magnitude. The gravitational force of a delivery room nurse is much stronger than the gravitational force of Jupiter (so much for Astrology). Whenever anyone is moving near others they are exerting a gravitational force on the other. It is so minisculy weak that it is immeasurable but present. And the force of gravity has bedeviled scientists for millennia. This article is the story of the search for what gravity is and how it works.
I should point out that I am NOT a scientist or engineer, nor have I received any education or training in science or engineering. This paper is the result of my readings on this subject in the past decades. Many academics, scientists, and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists and engineers’ entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. When writing for the general public this accuracy and thoroughness can often lead to less understandability. I believe it is essential for all laypersons to grasp the concepts of within this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.
The Ages of Physics
Science in human history can be broken down into three ages; Mythological, Aristotelian, and Galilean. Each age represents a different way to explain how and why the universe works the way it does.
Mythological Age
Before any formalization of science, people explained the ways of the universe through stories we refer to as myths. Their explanations were usually in the form of the Gods being displeased and causing bad things to happen, the Gods being please and causing good things to happen, and the Gods being indifferent and normal things happened. Although minor science was done (the Egyptians and the Babylonians come to mind) there was no systematic approach to determine why and how the universe worked.
Aristotelian Age
The Ancient Greeks were the first people to develop a systematic approach to the question as to why and how the universe worked. They utilized a philosophical approach as they thought about the question and developed logical reasoning to derive an answer. So, if their answer made logical sense it must be correct. They had no inclination to challenge their answer through observation or experimentation. The pinnacle of this approach was with the Philosopher Aristotle (for whom the age is named). Although some Ancient Greek philosophers did minor observations and experiments this was not the acceptable means of proving your answers.
Galilean Age
Galileo Galilei was the first truly modern scientist, as he approached science by observing nature, performing experiments, developing a hypothesis utilizing mathematics, and testing his hypothesis to determine if it was correct. He was so good at this, and so correct, that other scientists adopted his methods as the way to do science. So much so that scientist who utilized these methods were known as “Natural Philosophers”, and the Ancient Greek methods practitioners became known as simply “Philosophers”.
Background
The Four Forces of Nature
There are the four basic forces in nature. They were created at the time of the Big Bang and separated from themselves very shortly after they were created. This paper is about the Gravitational force, with the other forces being a focus in another paper (Atomic Physics).
- Electro-Magnetic Force - That acts between electrically charged particles. Electricity, magnetism, and light (the Electromagnetic Spectrum) are all produced by this force, and it has infinite range.
- Strong Force - That force that binds neutrons and protons together in the cores of atoms and is a very short-range force.
- Weak Force - That force that causes Beta decay, the release of atomic particles from an atom. Various atomic particles are formed by strong interactions but decay via the weak force. Like the strong force, the weak force is also a very short-range force.
- Gravity - That force that acts between all masses in the universe and it has infinite range. Gravity exists everywhere but is by many magnitudes weaker than all the other forces.
An Important Factor in the Advancement of Science
One of the most important factors in advancing science is the development of instruments to measure scientific phenomenon. Instruments that have a greater precision of length and/or a greater precision of time. Some early examples are the Refracting Telescope as refined by Galileo Galilei, the Reflecting Telescope as invented by Isaac Newton, the Pendulum Clock as invented by Christiaan Huygens, and the Microscope as invented by Zacharias Janssen and Hans Lippershey. Advancements in instrumentation led to advancements in science. This paper will not focus on these instrumentation advancements (except once – LIGO), rather on the advancements in science that occurred as a result.
The Motion of the Sun, Moon, and Planets
To understand the history of Gravity we need to know the history of Astronomy as it relates to Gravity. This relationship was with the motions of the Sun, Moon, and Planets, as gravity is responsible for these motions.
In the Mythological and Aristotelian age of science, gravity was thought to apply only to the Earth. The heavens were thought to be separate from the Earth, as they were the realm of the Gods and were perfect and incorruptible. The heavens, therefore, operated differently and were perfect and immutable while the Earth was imperfect and mutable. It was not until the Galilean age that this idea was dethroned by Isaac Newton when he proved that the same physical laws applied to the Heavens as well as the Earth. The ancient and medieval astronomers were also wedded to the idea that the Earth was the center of the Universe (geocentric). After all, when you observed the heavens you saw the stars, Planets, Moon, and Sun turning around the Earth, rising in the east to the southern meridian, then setting in the west. If the Earth were moving you should feel it, and perhaps fly off the Earth. So, the Earth was immovable and the heavens and other objects revolved around the Earth.
Yet the ancient astronomers noticed some peculiarities in the motion of the Sun, Moon, and Planets that were not perfect, and they spent over two thousand years trying to reconcile these motions with their perceived perfection of the heavens, rather than abandoning the perfection of the heavens. The phenomena that they could not make perfect are as follows.
Solar Analemma
 |
In astronomy, an Analemma is a diagram showing the variation of the position of the Sun in the sky over the course of a year, as viewed at a fixed time of day and from a fixed location on the Earth. The north–south component of the analemma is due to change of the Sun's declination caused by the tilt of the Earth's axis, and the east–west component is due to nonuniform rate of change of the Sun's right ascension, governed by combined effects of axial tilt and Earth's orbital eccentricity. The diagram has the form of a slender figure eight and can often be found on globes of the Earth. |
The ancient astronomers were puzzled by the analemma. They could write off the up and down motion of the Sun as simply the path that the Sun orbited around the Earth. But the back and forth motion did not fit into their view as of the Heavens bring perfect and incorruptible. If the Heavens were perfect and incorruptible there should be no back and forth motion, and the analemma should be a vertical line. The real reason for the analemma could be accounted for in the heliocentric (Sun Centered) view of the Solar System, with the Earth’s axis of rotation being tilted in relation to its orbital plane. This is known as The Celestial Equator and the Ecliptic. The ancient astronomers went to great lengths to explain the phenomena (see Eccentrics, Deferents, Epicycles, and Equants Oh My! later on in this paper) based upon the geocentric model of the solar system.
The Celestial Equator and the Ecliptic
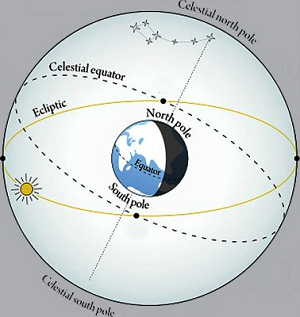 |
The Ecliptic is the circular path on the celestial sphere that the Sun appears to follow over the course of a year; it is the basis of the ecliptic coordinate system. The term also refers to the plane of this path, which is coplanar with Earth's orbit around the Sun (and hence the Sun's apparent orbit around Earth). The ecliptic is not normally noticeable from Earth's surface because Earth rotates, carrying the observer through the cycles of sunrise and sunset, which obscure the Sun's apparent motion against the background of fixed stars. Because Earth takes one year to orbit the Sun, the apparent position of the Sun takes one year to make a complete circuit of the ecliptic. With slightly more than 365 days in one year, the Sun moves a little less than 1° eastward every day. This small difference in the Sun's position against the stars causes any particular spot on Earth's surface to catch up with (and stand directly north or south of) the Sun about four minutes later each day than it would if Earth would not orbit; a day on Earth is therefore 24 hours long rather than the approximately 23-hour 56-minute sidereal day. Again, this is a simplification, based on a hypothetical Earth that orbits at uniform speed around the Sun. The actual speed with which Earth orbits the Sun varies slightly during the year, so the speed with which the Sun seems to move along the ecliptic also varies. For example, the Sun is north of the celestial equator for about 185 days of each year, and south of it for about 180 days. The variation of orbital speed accounts for part of the equation of time. |
The plane of Earth's orbit projected in all directions forms the reference plane known as the ecliptic. Here, it is shown projected outward (gray) to the celestial sphere, along with Earth's equator and polar axis (green). The plane of the ecliptic intersects the celestial sphere along a great circle (black), the same circle on which the Sun seems to move as Earth orbits it. The intersections of the ecliptic and the equator on the celestial sphere are the vernal and autumnal equinoxes (red), where the Sun seems to cross the celestial equator.
Lunar Apsidal Precession
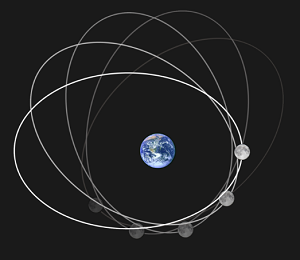 |
“In celestial mechanics, Apsidal Precession or orbital precession is the precession (rotation) of the orbit of a celestial body. More precisely, it is the gradual rotation of the line joining the apsides of an orbit, which are the points of closest and farthest approach. Perihelion is the closest point to the main body. The apsidal precession is the first derivative of the argument of periapsis, one of the six primary orbital elements of an orbit. “The ancient Greek astronomer Hipparchos noted the apsidal precession of the Moon's orbit; it is corrected for in the Antikythera Mechanism (circa 80 BCE) with the almost exactly accurate value of 8.88 years per full cycle, correct within 0.34%. The precession of the solar apsides was discovered in the eleventh century by al-Zarqali. The lunar apsidal precession was not accounted for in Claudius Ptolemy's Almagest, and as a group these precessions, the result of a plethora of phenomena, remained difficult to account for until the 20th century when the last unidentified part of Mercury's precession was precisely predicted in Albert Einstein's General Theory of Relativity.” |
The apsidal precession of the Moon was even more of a problem for the ancient astronomers to explain than the Solar analemma, as it had a more complex motion. The ancient astronomers went to great lengths to try to explain this phenomenon. They could not fully explain the apsidal precession of the Moon's orbit because of their geocentric view of the Solar System, but they tried (see Eccentrics, Deferents, Epicycles, and Equants Oh My! later on in this paper). It wasn’t until the Copernican Revolution, Kepler’s Laws of Planetary motion, and Newton’s Universal Gravitation that the apsidal precession of the Moon's orbit could be explained.
Venus and Mercury as Morning and Evening Stars
Venus and Mercury never strayed far from the sun, and they could be seen only at dawn or dusk. The enhanced photos below show their appearance at Dawn & Dusk:
 Planets at Dawn
|
 Planets at Dusk
|
Originally many ancient astronomers believed that Mercury and Venus at dawn and dust were separate planets. They soon realized that this was not true because they could not see either planet in both the dawn and dusk skies. They were either seen in the dawn sky OR the dusk sky, so they realized they were not separate planets. The other problem was the Greatest Elongation of Venus & Mercury above the Horizon. Venus moved further away from the horizon than Mercury. Additionally, if you plotted the position of these planets against the background stars they moved in an arc as seen below.
Greatest Elongation of Venus & Mercury above the Horizon.
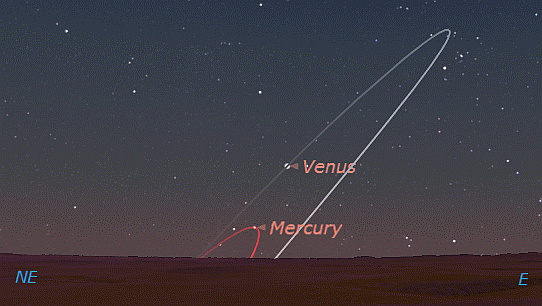
Again, the ancient astronomers went to convoluted explanations to explain the phenomena, and again it was because of their geocentric view of the Solar System that they failed to explain the motion of Mercury and Venus, but they tried (see Eccentrics, Deferents, Epicycles, and Equants Oh My! later on in this paper). It wasn’t until the Copernican Revolution, Kepler’s Laws of Planetary motion, and Newton’s Universal Gravitation that the motion of Mercury and Venus could be explained.
Mars Retrograde Motion
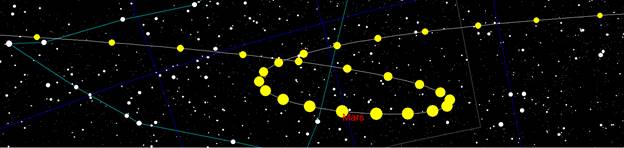
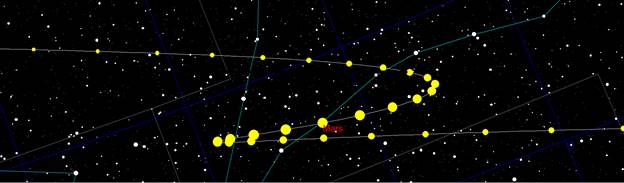
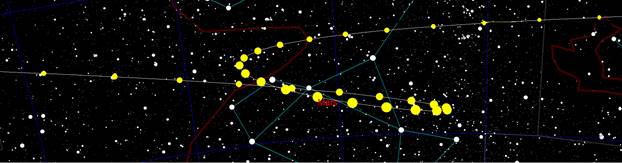
The motion of Mars drove the ancient astronomers into knots of convoluted explanations to account for its motion (See Eccentrics, Deferents, Epicycles, and Equants Oh My! for more information on the Aristotelian Age scientists attempt to explain this motion). The problem for them was that Mars would for a long period behave like Jupiter and Saturn in that it moved from west to east for many months in relation to the background stars. Mars would then stop, then start moving east to west, then stop and start moving from west to east. This motion, when plotted on a star chart could be a loop, and inverted “S”, or a loop within an inverted “S” (as the above illustration demonstrates). The problem for the ancient astronomers was that they had a geocentric (Earth Centered) view of the solar system. Once the Copernican heliocentric (Sun Centered) system was accepted and explained by Kepler’s Three Laws of Planetary Motion did Mar’s retrograde motion become understandable.
The Antikythera Mechanism
 |
The Antikythera mechanism is an ancient Greek analog computer and orrery used to predict astronomical positions and eclipses for calendar and astrological purposes decades in advance.] It could also track the four-year cycle of athletic games which was similar to an Olympiad, the cycle of the ancient Olympic Games. The device was found housed in the remains of a 340-millimetre (13 in) × 180-millimetre (7.1 in) × 90-millimetre (3.5 in) wooden box. It is a complex clockwork mechanism composed of at least 30 meshing bronze gears. A team led by Mike Edmunds and Tony Freeth at Cardiff University used modern computer x-ray tomography and high resolution surface scanning to image inside fragments of the crust-encased mechanism and read the faintest inscriptions that once covered the outer casing of the machine. Detailed imaging of the mechanism suggests that it had 37 gear wheels enabling it to follow the movements of the moon and the sun through the zodiac, to predict eclipses, and even to model the irregular orbit of the moon, where the moon’s velocity is higher in its perigee than in its apogee. This motion was studied in the 2nd century BC by astronomer Hipparchus of Rhodes, and it is speculated that he may have been consulted in the machine's construction. Its remains were found as one lump, later separated into three main fragments which are now divided into 82 separate fragments after conservation works. Four of these fragments contain gears, while inscriptions are found on many others. The largest gear is approximately 140 millimetres (5.5 in) in diameter and originally had 223 teeth. |
 |
The artefact was discovered on 17 May 1902 by archaeologist Valerios Stais, among wreckage retrieved from a wreck off the coast of the Greek island Antikythera. The instrument is believed to have been designed and constructed by Greek scientists and has been variously dated to about 87 BC, or between 150 and 100 BC, or to 205 BC, or to within a generation before the shipwreck, which has been dated to approximately 70-60 BC. The knowledge of this technology was lost at some point in antiquity, and technological works approaching its complexity and workmanship did not appear again until the development of mechanical astronomical clocks in Europe in the fourteenth century. All known fragments of the Antikythera mechanism are kept at the National Archaeological Museum in Athens, along with a number of artistic reconstructions of how the mechanism may have looked. |
|
The Antikythera mechanism was an amazing feat of engineering and surprised archeologist as they did not believe that the Ancient Greeks were capable of creating this technology. In addition, the mathematics and science knowledge required was more precise than it was believed that the Ancient Greeks possessed. Although the Antikythera mechanism was accurate over shorter periods of time (a few years) it would slowly become inaccurate over longer periods of time, due to the Ancient Greeks model of planetary motions (geocentric and perfect circles). The main problem of the Aristotelian Age scientists was their insistence that all heavenly bodies revolved around the Earth in perfect circles. It wasn’t until the Copernican Revolution that placed the Sun at the center that motions of the Sun, Moon, and Planets were understandable. With Kepler’s Three Laws of Planetary Motion, their motions became mathematical and scientific. |
 |
This leads us to the greatest physicists, astronomers, and mathematicians in the development of Gravitational Physics.
Aristotle
Teaching Alexander the Great gave Aristotle many opportunities and an abundance of supplies. He established a library in the Lyceum which aided in the production of many of his hundreds of books, which were written on papyrus scrolls. The fact that Aristotle was a pupil of Plato contributed to his former views of Platonism, but, following Plato's death, Aristotle immersed himself in empirical studies and shifted from Platonism to empiricism. He believed all peoples' concepts and all of their knowledge was ultimately based on perception. Aristotle's views on natural sciences represent the groundwork underlying many of his works. Aristotle's views on physical science profoundly shaped medieval scholarship. Their influence extended from Late Antiquity and the Early Middle Ages into the Renaissance, and were not replaced systematically until the Enlightenment and theories such as classical mechanics. Some of Aristotle's zoological observations, such as on the hectocotyl (reproductive) arm of the octopus, were not confirmed or refuted until the 19th century. His works contain the earliest known formal study of logic, which was incorporated in the late 19th century into modern formal logic. In metaphysics, Aristotelianism profoundly influenced Jewish and Islamic philosophical and theological thought during the Middle Ages and continues to influence Christian theology, especially the Neoplatonism of the Early Church and the scholastic tradition of the Catholic Church. Aristotle was well known among medieval Muslim scholars, and has been revered as "The First Teacher". His ethics, though always influential, gained renewed interest with the modern advent of virtue ethics. All aspects of Aristotle's philosophy continue to be the object of active academic study today. Though Aristotle wrote many elegant treatises and dialogues – Cicero described his literary style as "a river of gold" – it is thought that only around a third of his original output has survived. |
Aristotle was the greatest thinker of Ancient Greece when it came to the physical sciences. He attempted to synthase and categorize the Greek’s knowledge of the physical sciences, as well as contributing many new ideas of his own. He utilized a philosophical approach in that he thought about the question and developed logical reasoning to derive an answer. So, if his answer made logical sense it must be correct. His observational evidence was rudimentary and not rigorous (in a modern scientific sense), and he was not inclined to challenge his answer through experimentation. He was wedded to the idea that the Earth was the center of the universe, and the heavenly universe was perfect while the earthly was imperfect. As such, he often reached the wrong conclusions. But he was so logical and through in his arguments that most people accepted his answers as gospel. So much so that with the rise of Christianity and the Catholic Church they incorporated his conclusions into their doctrines. Therefore, in the Middle Ages, to dispute Aristotle was to dispute the church.
This and many other factors led free thinkers and the scientific-minded disinclined to dispute Aristotle but to find ways to prove Aristotle correct. Some of them raised objections to Aristotle, but they were soon rejected or silenced. It was not until the Renaissance and Reformation that Aristotle’s reasoning and conclusion began to be challenged. And the Enlightenment Age saw the end of Aristotelian science.
“On the Heavens” is Aristotle's chief cosmological treatise: written in 350 BC it contains his astronomical theory and his ideas on the concrete workings of the terrestrial world. It should not be confused with the spurious work “On the Universe” (De Mundo, also known as On the Cosmos).
Aristotle’s contributions (in a negative sense) to Gravitational Physics were his ideas on moving and falling bodies (which were totally wrong), and the geocentric view of the universe (which was also totally wrong). His contributions stymied other scientific ideas for over two thousand years.
Other Greeks
Anaximander of Miletus
 |
Anaximander (c.?610 – c.?546 BC) was a pre-Socratic Greek philosopher who lived in Miletus,a city of Ionia (in modern-day Turkey). He belonged to the Milesian school and learned the teachings of his master Thales. He succeeded Thales and became the second master of that school where he counted Anaximenes and, arguably, Pythagoras amongst his pupils. Little of his life and work is known today. According to available historical documents, he is the first philosopher known to have written down his studies, although only one fragment of his work remains. Fragmentary testimonies found in documents after his death provide a portrait of the man. He was an early proponent of science and tried to observe and explain different aspects of the universe, with a particular interest in its origins, claiming that nature is ruled by laws, just like human societies, and anything that disturbs the balance of nature does not last long. Like many thinkers of his time, Anaximander's philosophy included contributions to many disciplines. In astronomy, he attempted to describe the mechanics of celestial bodies in relation to the Earth. In physics, his postulation that the indefinite (or apeiron) was the source of all things led Greek philosophy to a new level of conceptual abstraction. His knowledge of geometry allowed him to introduce the gnomon in Greece. He created a map of the world that contributed greatly to the advancement of geography. He was also involved in the politics of Miletus and was sent as a leader to one of its colonies. |
Anaximander of Miletus is a pre-Aristotle Greek who broke complete from the scientific beliefs of his time. Anaximander is often called the first scientist because he was the first to suggest that order in the world was due to natural forces, not supernatural ones. He is the first person known to understand that the Earth floats in space; to believe that the sun, the moon, and the stars rotate around it—seven centuries before Ptolemy; to argue that all animals came from the sea and evolved; and to posit that universal laws control all change in the world. Anaximander taught Pythagoras, who would build on Anaximander’s scientific theories by applying mathematical laws to natural phenomena.
Aristarchus of Samos
 |
Aristarchus of Samos (Greek: c. 310 – c. 230 BC) was an ancient Greek astronomer and mathematician who presented the first known model that placed the Sun at the center of the known universe with the Earth revolving around it (see Solar system). He was influenced by Philolaus of Croton, but Aristarchus identified the "central fire" with the Sun, and he put the other planets in their correct order of distance around the Sun. Like Anaxagoras before him, he suspected that the stars were just other bodies like the Sun, albeit further away from Earth. He was also the first one to deduce the rotation of earth on its axis. His astronomical ideas were often rejected in favor of the incorrect geocentric theories of Aristotle and Ptolemy. Nicolaus Copernicus attributed the heliocentric theory to Aristarchus. |
Aristarchus of Samos was important because he was the first Greek astronomer and mathematician after Aristotle who challenged Aristotle’s geocentric model of the universe with his own heliocentric model. Other ancient Greek astronomers and mathematicians also made discoveries that were at odds with Aristotle’s ideas. Due to Aristotle’s almost demigod status Aristarchus and the others were disparaged and essentially ignored. The great Greek mathematician and engineer Archimedes of Syracuse (287 BCE - 212 BCE) criticized Aristarchus' discovery, and Hipparchus of Nicea (190 BCE - 120 BCE), the most respected and talented Greek astronomer in antiquity put an end to Aristarchus’ theory by saying that the geocentric model better explained his observations than did the model of Aristarchus. As a result, Aristarchus heliocentric idea was often rejected in favor of the incorrect geocentric theories of Aristotle and Ptolemy. However, over 1700 years later Nicolaus Copernicus attributed Aristarchus heliocentric theory to the development of his own heliocentric theory.
Hipparchus of Nicea
 |
Hipparchus of Nicaea (c. 190 – c. 120 BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of precession of the equinoxes. Hipparchus was born in Nicaea, Bithynia (now Iznik, Turkey), and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer at least from 162 to 127 BC. Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and by Meton of Athens (5th century BC), Timocharis, Aristyllus, Aristarchus of Samos and Eratosthenes, among others. He developed trigonometry and constructed trigonometric tables, and he solved several problems of spherical trigonometry. With his solar and lunar theories and his trigonometry, he may have been the first to develop a reliable method to predict solar eclipses. His other reputed achievements include the discovery and measurement of Earth's precession, the compilation of the first comprehensive star catalog of the western world, and possibly the invention of the astrolabe, also of the armillary sphere, which he used during the creation of much of the star catalogue. |
Hipparchus data on the stars positions and brightness, and the planetary positions, were basis for astronomical studies for the next 17 centuries. His invention of the astrolabe was the primary means of measuring star and planetary positions until the invention of the telescope. Using Eratosthenes estimate of the diameter of the Earth Hipparchus was able to calculate the Earth-Moon distance to about 1% of its actual value. All of this was of great value for future Gravitational Physics scientific endeavors.
Claudius Ptolemy
 |
Claudius Ptolemy (Greek:; c. AD 100 – c.?170) was a Greco-Roman mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in the city of Alexandria in the Roman province of Egypt, wrote in Koine Greek, and held Roman citizenship. The 14th-century astronomer Theodore Meliteniotes gave his birthplace as the prominent Greek city Ptolemais Hermiou in the Thebaid. This attestation is quite late, however, and, according to Gerald Toomer, the translator of his Almagest into English, there is no reason to suppose he ever lived anywhere other than Alexandria. He died there around AD 168. Ptolemy wrote several scientific treatises, three of which were of importance to later Byzantine, Islamic and European science. The first is the astronomical treatise now known as the Almagest, although it was originally entitled the Mathematical Treatise (Mathematike Syntaxis) and then known as the Great Treatise (He Megále Syntaxis). The second is the Geography, which is a thorough discussion of the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian natural philosophy of his day. This is sometimes known as the Apotelesmatika but more commonly known as the Tetrabiblos from the Greek meaning "Four Books" or by the Latin Quadripartitum. |
Ptolemy’s major contribution to Gravitational Physics was that his geocentric solar system model could more accurately explain the motions of heavenly bodies then the earlier models. It became the model for understanding the structure of the solar system for over a thousand years. The Ptolemaic model accounted for the apparent (retrograde) motions of the planets in a very direct way, by assuming that each planet moved on a small sphere or circle, called an epicycle, that moved on a larger sphere or circle, called a deferent. The stars, it was assumed, moved on a celestial sphere around the outside of the planetary spheres.
Ptolemy's fame comes partly from what he figured out, but his influence was largely because he wrote a great summary of everything known about astronomy. Ptolemy insisted that the job of the astronomer was to explain the motions of the wanderers using only uniform circular motion - the kind of motion that most gears and wheels show.
Eccentrics, Deferents, Epicycles, and Equants Oh My!
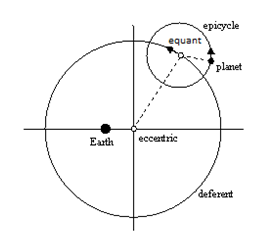
The earliest astronomers imagined the distant stars to be embedded in a crystal sphere, centered on the (presumed stationary) earth, and rotating uniformly. This is consistent with the apparent fact that the stars all move in unison and have constant brightness. The Sun, moon, and planets, however, do not move in unison, nor are their individual apparent motions uniform. In addition, the brightnesses of the planets vary, which suggests that their distances from the earth are not constant. The ancients sought to represent the paths of these objects as circles, but even for the relatively simple annual motion of the Sun they found it necessary to assume that the circular path was centered on a point - called the eccentric - some distance away from the Earth. Ptolemy proposed a model based on the Geocentric universe of Aristotle and assumed uniform circular motion of the heavens. Because of this, his model couldn't accurately predict the motion of the Sun, Moon, and Planets. He needed to find another way explain their motions. Ptolemy used an ingenious contrivance called the epicycle. The planets moved around on these small circles, which they themselves moved along a larger circular orbit called the deferent. This allowed for varying planet motions, as seen on Earth while maintaining (nearly) spherical motion and constant velocities. A small adjustment was made to move the Earth from the center of the deferent, defined as the equant, as the location of pure constant motion. This was the Ptolemaic Model and is depicted in the figure to the left. The Ptolemaic Model was more accurate than the other models but was not accurate over a long period of time.
Nicolaus Copernicus
  |
Nicolaus Copernicus (Polish: Mikolaj Kopernik; German: Nikolaus Kopernikus; Niklas Koppernigk; 19 February 1473 – 24 May 1543) was a Renaissance- and Reformation-era mathematician and astronomer who formulated a model of the universe that placed the Sun rather than the Earth at the center of the universe, likely independently of Aristarchus of Samos, who had formulated such a model some eighteen centuries earlier. The publication of Copernicus' model in his book De Revolutionibus Orbium Coelestium (On the Revolutions of the Celestial Spheres), just before his death in 1543, was a major event in the history of science, triggering the Copernican Revolution and making an important contribution to the Scientific Revolution. Copernicus was born and died in Royal Prussia, a region that had been part of the Kingdom of Poland since 1466. A polyglot and polymath, he obtained a doctorate in canon law and was also a mathematician, astronomer, physician, classics scholar, translator, governor, diplomat, and economist. In 1517 he derived a quantity theory of money – a key concept in economics – and in 1519 he formulated an economics principle that later came to be called Gresham's law. |
Copernicus was the first Natural Philosopher1 who challenged Aristotle after the Middle Ages. His heliocentric theory (Sun Centered) was published while Copernicus was on his deathbed in 1543 (although he had written it many years earlier). By 1533 Copernicus's work was nearing its definitive form, and rumors about his theory had reached educated people all over Europe. Despite urgings from many quarters, Copernicus delayed publication of his book, perhaps from fear of criticism—a fear delicately expressed in the subsequent dedication of his masterpiece to Pope Paul III. Scholars disagree on whether Copernicus's concern was limited to possible astronomical and philosophical objections, or whether he was also concerned about religious objections. But he was concerned about the personal repercussions of challenging church doctrine. His book “On the Revolutions of the Celestial Spheres” was the first major scholarly work based on observations and calculations that demonstrated that Aristotle and Ptolemy were wrong about the structure of the solar system.
Copernicus incorrectly believed that the planets moved in circles. However, his heliocentric theory accounted for the apparent motions of the planets, the Solar Analemma, the Lunar Apsidal Precession, Venus and Mercury as Morning and Evening Stars, and the Mars Retrograde Motion in a much simpler fashion than the geocentric system.
It started the “Copernican Revolution” in science in which other scientists rallied behind, most notably Galileo. The crack in the door had been opened for modern science to begin.
1A Philosopher is someone who practices philosophy, which involves the rational inquiry into areas that are outside either theology or science. Natural Philosophers studied the natural world and the physical universe that was dominant before the development of modern science. It is considered to be the precursor of natural science whose practitioners became known as Scientists. A Theologian is one studies the nature of the divine. Theology is taught as an academic discipline, typically in universities, seminaries, and schools of divinity.
Tycho Brahe
  |
Tycho Brahe (born Tyge Ottesen Brahe (Danish: 14 December 1546 – 24 October 1601) was a Danish nobleman, astronomer, and writer known for his accurate and comprehensive astronomical and planetary observations. He was born in the then Danish peninsula of Scania. Well known in his lifetime as an astronomer, astrologer and alchemist, he has been described as "the first competent mind in modern astronomy to feel ardently the passion for exact empirical facts." His observations were some five times more accurate than the best available observations at the time. An heir to several of Denmark's principal noble families, he received a comprehensive education. He took an interest in astronomy and in the creation of more accurate instruments of measurement. As an astronomer, Tycho worked to combine what he saw as the geometrical benefits of the Copernican system with the philosophical benefits of the Ptolemaic system into his own model of the universe, the Tychonic system. Furthermore, he was the last of the major naked-eye astronomers, working without telescopes for his observations. In his De Nova Stella (On the New Star) of 1573, he refuted the Aristotelian belief in an unchanging celestial realm. His precise measurements indicated that "new stars" (Stellae Novae, now known as supernovae), in particular that of 1572, lacked the parallax expected in sublunar phenomena and were therefore not tailless comets in the atmosphere as previously believed but were above the atmosphere and beyond the moon. Using similar measurements he showed that comets were also not atmospheric phenomena, as previously thought, and must pass through the supposedly immutable celestial spheres. King Frederick II granted Tycho an estate on the island of Hven and the funding to build Uraniborg, an early research institute, where he built large astronomical instruments and took many careful measurements, and later Stjerneborg, underground, when he discovered that his instruments in Uraniborg were not sufficiently steady. On the island (where he behaved autocratically toward the residents) he founded manufactories, such as a paper mill, to provide material for printing his results. After disagreements with the new Danish king, Christian IV, in 1597, he went into exile, and was invited by the Bohemian king and Holy Roman Emperor Rudolph II to Prague, where he became the official imperial astronomer. He built an observatory at Benátky nad Jizerou. There, from 1600 until his death in 1601, he was assisted by Johannes Kepler, who later used Tycho's astronomical data to develop his three laws of planetary motion. Tycho's body has been exhumed twice, in 1901 and 2010, to examine the circumstances of his death and to identify the material from which his artificial nose was made. The conclusion was that his death was likely caused by a burst bladder, and not by poisoning as had been suggested, and that the artificial nose was more likely made of brass than silver or gold, as some had believed in his time. |
|
|
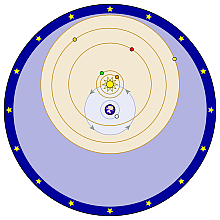 The Tychonic System. Tycho’s planetary model correctly saw the Moon as orbiting Earth, and the planets as orbiting the Sun, but erroneously considered the Sun to be orbiting the Earth as depicted to the left. In this depiction of the Tychonic system, the objects on blue orbits (the Moon and the Sun) revolve around the Earth. The objects on orange orbits (Mercury, Venus, Mars, Jupiter, and Saturn) revolve around the Sun. Around all is a sphere of fixed stars. |
Without Tycho, there could be no Kepler. And without Kepler, there would be no Three Laws of Planetary Motion. And without these laws, the motions of the Planets were not understandable. Tycho was the greatest naked-eye astronomer in history. His measurement of the Stars and Planets positions were as precise as was possible with the human eye. So precise that they could be used for mathematical purposes and scientific explanations. Unfortunately, he still held to the belief of the Earth at the center of the solar system and came up with an explanation, named the Tychonic System, that tried to meld heliocentric (Sun Centered) and geocentric (Earth Centered) systems. In this he was wrong.
Johannes Kepler
  |
Johannes Kepler (German: December 27, 1571 – November 15, 1630) was a German mathematician, astronomer, and astrologer. Kepler is a key figure in the 17th-century scientific revolution. He is best known for his laws of planetary motion, based on his works Astronomia Nova, Harmonices Mundi, and Epitome of Copernican Astronomy. These works also provided one of the foundations for Isaac Newton's theory of universal gravitation. Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, invented an improved version of the refracting telescope (the Keplerian telescope), and was mentioned in the telescopic discoveries of his contemporary Galileo Galilei. He was a corresponding member of the Accademia dei Lincei in Rome. Kepler lived in an era when there was no clear distinction between astronomy and astrology, but there was a strong division between astronomy (a branch of mathematics within the liberal arts) and physics (a branch of natural philosophy). Kepler also incorporated religious arguments and reasoning into his work, motivated by the religious conviction and belief that God had created the world according to an intelligible plan that is accessible through the natural light of reason. Kepler described his new astronomy as "celestial physics", as "an excursion into Aristotle's Metaphysics", and as "a supplement to Aristotle's On the Heavens", transforming the ancient tradition of physical cosmology by treating astronomy as part of a universal mathematical physics. In 1594, Kepler became a professor of mathematics, as well as district mathematician and calendar maker. In his spare time, he continued to study astronomy and astrology (which were virtually the same thing back then). In search of the most detailed notes about the paths of the planets, Kepler contacted astronomer Tycho Brahe. A wealthy Danish nobleman, Brahe built an observatory in Prague where he tracked the motions of the planets and maintained the most accurate positional observations of the solar system objects and the stars that were possible for his time. In 1600, Brahe invited Kepler to come work with him. Brahe, however, became suspicious and unwilling to share his notes with his assistant. Instead, he assigned Kepler to solve the mystery of Mars, one of the most puzzling problems in astronomy at the time. Ironically, the detailed records of this challenging planet were the tools Kepler needed to understand planetary motions. When Brahe died in 1601, Kepler managed to acquire Brahe's observations before his family could use them to their financial benefit. Kepler original thought it would only take him several days to determine planetary motions once he had all of Tycho’s observations. Almost two decades later he finished his calculations and he had the Three Laws of Planetary Motion. |
It took him several years to determine the planets travel on elliptical paths, which is known as Kepler's First Law.
Kepler also struggled with changes in the velocities of the planets. He realized that a planet moved slower when it was farther away from the sun than it did when nearby. Once he understood that planets traveled in ellipses, he determined that an invisible line connecting the sun to a planet covered an equal amount of area over the same amount of time. He posited this, his Second Law, along with his first, which he published in 1609.
Kepler's Third Law was published a decade later which recognized that the relationship between the period of two planets, the time they take to orbit the Sun is connected to their distance from the sun. These three laws are illustrated below.
Kepler’s Laws of Planetary Motion
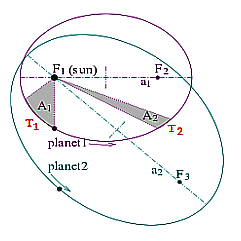 |
|
With the publication of the Three Laws of Planetary Motion, it was obvious to the scientific minds of the time that the heliocentric model of the solar system as defined by Kepler was the only correct model.
Galileo Galilei
   |
Galileo Galilei (Italian: 15 February 1564 – 8 January 1642) was an Italian polymath. Galileo is a central figure in the transition from natural philosophy to modern science and in the transformation of the scientific renaissance into a scientific revolution. Galileo's championing of heliocentrism and Copernicanism was controversial during his lifetime, when most subscribed to either Geocentrism or the Tychonic system. He met with opposition from astronomers, who doubted heliocentrism because of the absence of an observed stellar parallax. The matter was investigated by the Roman Inquisition in 1615, which concluded that heliocentrism was "foolish and absurd in philosophy, and formally heretical since it explicitly contradicts in many places the sense of holy scripture." Galileo later defended his views in Dialogue Concerning the Two Chief World Systems, which appeared to attack Pope Urban VIII and thus alienated him and the Jesuits, who had both supported Galileo up until this point. He was tried by the Inquisition, found "vehemently suspect of heresy", and forced to recant. He spent the rest of his life under house arrest. While under house arrest, he wrote one of his best-known works, Two New Sciences, in which he summarized work he had done some forty years earlier on the two sciences now called kinematics and strength of materials. Galileo studied speed and velocity, gravity and free fall, the principle of relativity, inertia, projectile motion and also worked in applied science and technology, describing the properties of pendulums and "hydrostatic balances", inventing the thermoscope and various military compasses, and using the telescope for scientific observations of celestial objects. His contributions to observational astronomy include the telescopic confirmation of the phases of Venus, the discovery of the four largest satellites of Jupiter, the observation of Saturn’s rings (though he could not see them well enough to discern their true nature) and the analysis of Sunspots. Known for his work as astronomer, physicist, engineer, philosopher, and mathematician, Galileo has been called the "Father of Observational Astronomy", the "Father of Modern Physics", the "Father of the Scientific Method", and even the "Father of Science".
|
Galileo Galilei was the first major scientist that challenged the Aristotelian method of science. He believed that “Observation and Experimentation” should be the basis of all science, and that the science was more important than the philosophy or theology. If philosophy or theology did not agree with the science, then the philosophy or theology needed to be modified or discarded.
He challenged all Aristotelian science and proved with observation and experimentation that Aristotle was incorrect in many physical phenomena. He also answered many unanswerable problems (within his time) in physical phenomena through observation and experimentation. He developed a scientific method that was the basis for all future scientific investigation, and he applied mathematics to science.
His defense of the Copernican revolution shook the chokehold of religion over science and allowed many other scientists to defend the Copernican revolution. “The Dialogue Concerning the Two Chief World Systems” published in 1632 is the book by Galileo Galilei comparing the Copernican system with the traditional Ptolemaic system, and it was a significant factor in establishing the Copernican system.
“The Discourses and Mathematical Demonstrations Relating to Two New Sciences”, published in 1638, was Galileo's final book and a scientific testament covering much of his work in physics over the preceding thirty years. It was much referred to by the succeeding generation of physicists. Without Galileo’s discarding of Aristotelian science, and loosening the chokehold of religion over science, it would not have been possible to proceed with Gravitational Physics.
His contribution to Gravitational Physics was in the acceleration of falling bodies, and the trajectories of moving bodies (parabolas). During the course of his scientific endeavors, Galileo became interested in the motion of falling bodies. Aristotle had postulated that heavier bodies fall faster than lighter bodies (think of a feather and a stone falling together), and Aristotle came up with a rational and logical explanation for this, which was totally wrong. Galileo set out to determine the truth. He knew he could not directly measure falling bodies, as they fell too fast for him to obtain measurements. He reasoned that if he rolled spheres of different weights down a gently inclined plane they would move slower. He was then able to measure the speed of these rolling spheres. His experiments discovered that both heaver and lighter spheres rolled at the same rate. He was even able to measure the rate of acceleration of the spheres as thirty-two feet per second per second. As Galileo increased the slope of the inclined plane rate of acceleration still held if the slope were 15o, 30o, or 45o. He, therefore, reasoned that a 900 slope (straight down) the rate of acceleration would still hold. Gravity was uniform for all weights.
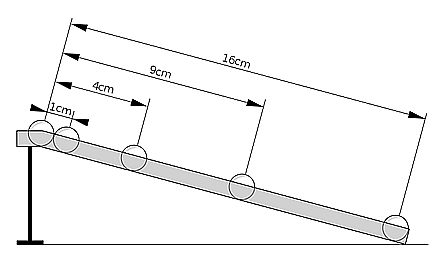
Gravity accelerates a mass toward the ground by increasing its speed by 32 feet per second with each passing second. So, for example, if you drop a ball off of a tall building (and if you ignore wind resistance, which retards acceleration as the ball gains speed), you will find that the ball is traveling at 32 fps after 1 second; 64 fps after 2 seconds, 96 fps after 3 seconds, and so on. Another way of reporting this is that the ball’s speed increases by 32 feet-per-second with each second. Or, in other words: The rate increases at an acceleration of 32 feet per second per second. This is written as 32 ft/s2.
Galileo utilized this discovery to determine the motions of moving bodies such as cannon balls. He discovered that their motion was a parabola that also obeyed his acceleration formula when they began to fall.
These scientific results and Galileo’s other works were very important to Isaac Newton in the development of Newton’s Law of Universal Gravitation and his Three Laws of Motion.
Galileo’s Character
Galileo seems to have led a fairly normal lifestyle for his time, and he had many friends, as well as contacts with other Natural Philosophers. However, when Galileo believed himself to be right he could become stubborn, persistent and argumentative in expressing his opinions. This often led him into conflicts with authority, and in his time authority was mainly the Catholic Church and the Princes of the principalities of Italy. He believed that if science conflicted with church doctrine, then church doctrine need to be changed or replaced. Unfortunately, Galileo lived during the time of the Protestant Reformation1, and the Catholic Church was not receptive to changing its doctrine. Galileo persisted and eventually incurred the ire of the Pope and he was forced to face the Inquisition2 in 1633. At the conclusion of the Inquisition, he was forced to recant his opinion and was placed under house arrest for the rest of his life. While under house arrest he completed his book “Two New Sciences”, in which he summarized work he had done some forty years earlier on the two sciences now called kinematics and strength of materials.
As to his personal life, Galileo had a mistress, Marina Gamba, with whom he had three children. During one of his frequent trips to Venice, Galileo met a young woman named Marina di Andrea Gamba and started a relationship with her. She moved into his house in Padua and bore him three children: Virginia (16 August 1600 – 1634), later Sister Maria Celeste; Livia (1601–1659), later Sister Arcangela; and Vincenzo (1606–1649). In none of the three baptismal records is Galileo named as the father. Virginia was described as "daughter by fornication of Marina of Venice," with no mention of the father; on Livia's baptismal record the name of the father was left blank; Vincenzo's baptismal record announced "father uncertain" (Galileo's Daughter 24, Dava Sobel, 1999). Galileo's position as a professor and his many friendships among the Venetian nobility probably made it unwise for him to figure officially as the children's father.
When Galileo left Padua for good in 1610 to take up his position
at the Medici court in Florence, he took the two daughters with
him but left their mother behind with 4 year-old Vincenzo, who
joined his father in Florence a few years later. With Marina no
longer in the family, Galileo put his two daughters in a convent
and managed to have Vincenzo legitimated by the Grand Duke of
Tuscany. In his 1619 request for this, Galileo declared that at
the time of his cohabitation with Marina, she "had never been
married" and was "already dead" at the drawing up of the act.
Maria Celeste maintained contact with her father throughout her
entire life through letters. Although none of Galileo's letters
are known to have survived, 120 of Maria Celeste's exist. These
letters, written from 1623 to 1634, depict a woman with incredible
brilliance, industry, sensibility and a deep love for her father.
Maria Celeste died of dysentery in 1634.
1The Reformation, specifically referred to as the Protestant Reformation, was a schism in Western Christianity initiated by Martin Luther and continued by John Calvin, Huldrych Zwingli, and other early Protestant Reformers in 16th-century Europe. It is usually considered to have started with the publication of the Ninety-five Theses by Martin Luther in 1517 and lasted until the end of the Thirty Years' War with the Peace of Westphalia in 1648.
2The Inquisition was a group of institutions within the government system of the Catholic Church whose aim was to combat heresy. It started in 12th-century France to combat religious dissent, in particular the Cathars and the Waldensians. Other groups investigated later included the Spiritual Franciscans, the Hussites (followers of Jan Hus) and the Beguines. Beginning in the 1250s, inquisitors were generally chosen from members of the Dominican Order, replacing the earlier practice of using local clergy as judges. The term Medieval Inquisition covers these courts up to mid-15th century.
During the Late Middle Ages and early Renaissance, the concept and scope of the Inquisition significantly expanded in response to the Protestant Reformation and the Catholic Counter-Reformation. It expanded to other European countries, resulting in the Spanish Inquisition and Portuguese Inquisition. The Spanish and Portuguese operated inquisitorial courts throughout their empires in Africa, Asia, and the Americas (resulting in the Peruvian Inquisition and Mexican Inquisition). The Spanish and Portuguese inquisitions focused particularly on the issue of Jewish anusim and Muslim converts to Catholicism, partly because these minority groups were more numerous in Spain and Portugal than in many other parts of Europe, and partly because they were often considered suspect due to the assumption that they had secretly reverted to their previous religions.
Except within the Papal States, the institution of the Inquisition was abolished in the early 19th century, after the Napoleonic Wars in Europe and after the Spanish American wars of independence in the Americas. The institution survived as part of the Roman Curia, but in 1908 was given the new name of "Supreme Sacred Congregation of the Holy Office". In 1965 it became the Congregation for the Doctrine of the Faith.
Isaac Newton
 |
Sir Isaac Newton (English: 25 December 1642 – 20 March 1726/27) was an mathematician, astronomer, theologian, author and physicist (described in his own day as a "Natural Philosopher") who is widely recognized as one of the most influential scientists of all time and a key figure in the scientific revolution. His book Philosophić Maturalis Principia Mathematica ("Mathematical Principles of Natural Philosophy"), first published in 1687, laid the foundations of classical mechanics. Newton also made pathbreaking contributions to optics, and he shares credit with Gottfried Wilhelm Leibniz for developing the infinitesimal calculus. Newton's Principia formulated the Laws of Motion and Universal Gravitation that dominated scientists' view of the physical universe for the next three centuries. By deriving Kepler’s Laws of Planetary Motion from his mathematical description of gravity, and using the same principles to account for the trajectories of comets, the tides, the precession of the equinoxes, and other phenomena, Newton removed the last doubts about the validity of the heliocentric model of the solar system and demonstrated that the motion of objects on earth and of celestial bodies could be accounted for by the same principles. Newton's theoretical prediction that the earth is shaped as an oblate spheroid was later vindicated by the geodetic measurements of Maupertuis, la Condamine, and others, thus convincing most continental European scientists of the superiority of Newtonian mechanics over the earlier system of Descartes. Newton also built the first practical reflecting telescope and developed a sophisticated theory of colour based on the observation that a prism decomposes white light into the colours of the visible spectrum. Newton's work on light was collected in his highly influential book Opticks, first published in 1704. He also formulated an empirical law of cooling, made the first theoretical calculation of the speed of sound, and introduced the notion of a Newtonian fluid. In addition to his work on calculus, as a mathematician newton contributed to the study of power series, generalised the binomial theorem to non-integer exponents, developed a method for approximating the roots of a function, and classified most of the cubic plane curves. Newton was a fellow of Trinity College and the second Lucasian Professor of Mathematics at the university of Cambridge. He was a devout but unorthodox Christian, who privately rejected the doctrine of the trinity and who, unusually for a member of the Cambridge faculty of the day, refused to take holy orders in the church of England. Beyond his work on the mathematical sciences, Newton dedicated much of his time to the study of alchemy and biblical chronology, but most of his work in those areas remained unpublished until long after his death. Politically and personally tied to the Whig party, Newton served two brief terms as member of Parliament for the University of Cambridge, in 1689–90 and 1701–02. He was knighted by Queen Anne in 1705 and he spent the last three decades of his life in London, serving as Warden (1696–1700) and Master (1700–1727) of the royal mint, as well as President of the Royal Society (1703–1727). |
“Nature and Nature's laws lay hid in night: God said, Let Newton be! and all was light.” - Alexander Pope
It is hard to understate Isaac Newton’s contributions to science. Even Albert Einstein thought of Newton as the greatest scientist that ever lived, and in a recent poll most scientists agreed that is was Newton first, Einstein second, and Maxwell third in importance.
At the time Isaac Newton was alive the Galilean revolution was still being fought by many influential people. Aristocrats, Theologians, Monied Interests, and some Scientists felt that the Galilean revolution would upset the established order (which it did) and they may lose their power, prestige, and perhaps their fortunes. By the time of Newton’s death, the Galilean revolution had been won in no small part because of the science of Isaac Newton.
Isaac Newton was a key figure in the “Age of Reason”. European politics, philosophy, science and communications were radically reoriented during the course of the “long 18th century” (1685-1815) as part of a movement referred to by its participants as the age of reason, or simply the enlightenment. Enlightenment thinkers in Britain, in France and throughout Europe questioned traditional authority and embraced the notion that humanity could be improved through rational change. The enlightenment produced numerous books, essays, inventions, scientific discoveries, laws, wars, and revolutions. The American and French revolutions were directly inspired by enlightenment ideals and respectively marked the peak of its influence and the beginning of its decline. The enlightenment ultimately gave way to 19th-century romanticism.
Newton’s greatest contributions to science were in his Mathematical Principles of Natural Philosophy, (often referred to as simply the Principia), his creation and development of the mathematics of Fluxions (Calculus), and his work on Opticks. Newton’s contribution to Gravitational Physics was through his Principia. “Mathematical Principles of Natural Philosophy” is the three-volume work about his laws of motion and universal gravitation that was published in Latin in 1687. It is considered one of the most important works of science in history, along with his two other books.
In 1666 Newton became interested in the problem of gravitation. The story of his sitting under the apple tree and having the Apple fall upon his head is apparently untrue. However, it is not far off. As related by Newton’s niece's husband after Newton’s death he told a story that Newton supposedly told him. There is no direct proof of this story but as it came from a close family member who had lived with Newton for many years, and it may be true. Newton had a habit of when he was in deep thought of taking walks through the fields and orchards around Cambridge and ponder the problem he was considering. On one particular day, he was walking past the apple orchard thinking about the problem of the gravity, and more specifically the Orbit of the Moon. He noticed the daytime Moon in the same field of view as an apple tree. Upon stopping and pondering the problem an apple dropped off a tree branch in his same field of view of the Moon. He began to consider that perhaps the force of the Apple falling to the Earth was also the force of the Moon revolving around the Earth. He rushed back to his laboratory and began to calculate to determine if this could be true. Very quickly he had the answer, yes it was, and his calculations are now known as Universal Gravitation. He was able to calculate the orbit of the Moon and the other planets using his Universal Gravitation formula. Once he had satisfied to himself that his theory was correct he put it aside in a stack of papers on a shelf in his lab and went on to other problems. There it remained, untouched, for over twenty years. Twenty years later the members of the Royal Society (a newly formed society of English Natural Philosophers) became involved a heated discussion, almost resulting in blows among several members, about what the orbit of a planet would be if the gravity between them was inversely proportional to the square of its distance. Some believed it was a circle, while others believed it was an ellipse, or a parabola, or a hyperbola as the Conic Section explanation below demonstrates. No one could come up with any scientific explanation of what the orbit would be, so they decided to consult with Newton to see if he could determine the answer.
Conic Section
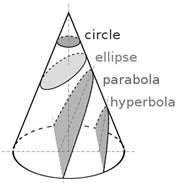
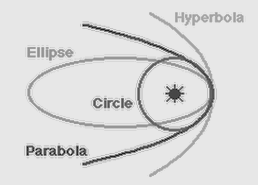
In mathematics, a Conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse and is of sufficient interest in its own right that it was sometimes called a fourth type of conic section. The conic sections have been studied by the ancient Greek mathematicians with this work culminating around 200 BC, when Apollonius of Perga undertook a systematic study of their properties
Newton was a very prickly character and very difficult to work with (more on that later) and they knew that writing a letter to Newton would elicit no response from him. They, therefore, decided to send someone to put the question to Newton. They all decided that Edmond Halley should be the person to go to Newton, as he was one of the most congenial Natural Philosopher that they knew. Indeed, he was often the peacemaker during the heated discussions that had led them to contact Newton. Halley, being a prudent man very carefully planned out how he would approach Newton on this question. He wrote to Newton explaining that he was planning to take a ride through the country over the summer season and as he would be passing by Cambridge he wondered if it would be alright if he could visit Newton and talk to him about the goings-on of the Royal Society. Much to his surprise, Newton responded positively, and they agreed to the few days in which Halley could visit Newton. At the start of the visit Halley, being a very smart man did not bring up the problem of the planetary orbits immediately. He waited a few days, and during one of his walks with Newton he mentioned the problem and wondered if Newton had a solution. Newton immediately responded that it was an ellipse. Holly was thunderstruck and blurted out how the question of how he knew that this was true. Newton responded that several years ago he had calculated it and solved the problem of the orbits of the moon and the planets. Holly asked if it would be possible for him to look at these calculations and learn about the solution. Newton responded that he did not know where the calculation was as he had filed them away many years ago. However, Newton volunteered to search for these calculations and send him a copy through the Postal Service. Holly departed shortly thereafter and eagerly awaited these calculations from Newton. After several months he had not received them, and he composed a very pleasant letter to Newton thanking him for his visit and wondering if perhaps the calculations may have been lost in the Postal Service (a common occurrence of that day). Newton responded that he was unable to find his calculations, but he was working on them again and would send a copy to Holly as soon as he was finished. A few weeks later Holly received the calculations and was thunderstruck again as the calculations showed Newton's Law of Universal Gravitation. Halley knew that this was one of the most important scientific discoveries in history. He wrote back to Newton and asked if he would publish these calculations. Newton responded that he was not very interested in doing this, as publishing in those days was a very laborious process that consumed much of the time of the author. Halley wrote back and said that he would be happy to do the laborious work with only Newton's guidance and approval of the final document. Newton agreed to this arrangement and Halley set about getting the calculations published. In Halley’s many discussions with Newton during this period he discovered that there was much, more much more than the Universal Gravitation calculations. He also discovered that Newton had worked out the laws of motion and the science of ballistics utilizing these calculations. Halley realized that all of this needed to be published but that it would be very time-consuming and expensive. In Halley‘s day, the author was responsible for paying the printer all of the cost of producing a book. Halley convinced the Royal Society that they should pay for the book, and he would do the manual efforts required to publish the book. Unfortunately, the Royal Society reneged on its promise to pay for the book and Halley, not a rich man, ended up paying for the publication costs out of his own small fortune.
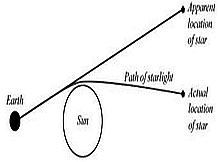
After nearly two years of intense work by Halley and Newton (he finally began to pitch in) the book was published. The Mathematical Principles of Natural Philosophy caused a great sensation not only in the scientific world but in the rest of the world. Not only had Newton defined Gravity the Laws of Motion and Ballistics, but he was the first scientist to prove that the laws of nature applied to the Heavens as well as the Earth. His Universal Gravitation also explained why Kepler’s Law of Planetary Motion worked. His proof that the heavens and earthly laws were the same caused a great change in the relationship of man to God and kick-started the Age of Enlightenment or sometimes known as The Age of Reason. After the publication, Newton was acknowledged as the greatest scientist who ever lived. Newton became almost a demigod and everything that Newton said was so was believed to be so. If other scientists disagree with Newton they were often ignored in favor of Newton’s ideas. This remained throughout the 18th century, and it wasn't until the scientific discoveries of the 19th century that Newton theories, other than gravitation and motion, would begin to be doubted. It wasn't until Einstein's publication in 1916 of his General Relativity that Newton's Universal Gravitation was doubted. With the proof of the deflection of starlight (discuss later under Einstein) Newton's Universal Gravitation and his Laws of Motion were overturned.
It should be noted that Newton's Universal Gravitation and his Three Laws of Motion still work perfectly on a smaller scale (molecular through earthly phenomena). When engineers and scientists are working on these scales they will often utilize Newton’s gravitation and motion laws as it is easier to calculate, and the differences between Newton’s gravitation and Einstein’s gravitation are too small to have any effect at these scales. However, scientists and engineers need to keep in mind that there is a difference and that sometimes the difference needs to be accounted for. This is especially true for spacecraft that are traveling between the planets. They generally use Newton’s Universal Gravitation and Laws of Motions to plot the course of the space probe. But once or twice in the trajectory of the space probe, they need to make a course correction to account for Einstein's General Relativity. Global positioning satellites and systems also need to account for Einstein's General Relativity to provide accurate information. This is also true for many scientific experiments in that they need to account for General Relativity to achieve the proper results. Below is a brief overview of Newton’s Universal Gravitation and his Three Laws of Motion, and a brief description of Calculus.
Newton’s Universal Gravitation
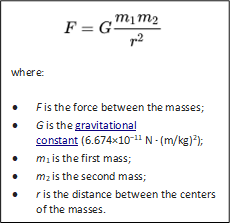 |
Newton's law of universal gravitation states that a particle attracts every other particle in the universe with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This is a general physical law derived from empirical observations by what Isaac Newton called inductive reasoning. It is a part of classical mechanics and was formulated in Newton's work Philosophić Naturalis Principia Mathematica ("the Principia"), first published on 5 July 1686. When Newton's book was presented in 1686 to the Royal Society, Robert Hooke made a claim that Newton had obtained the inverse square law from him. In today's language, the law states: Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. The first test of Newton's theory of gravitation between masses in the laboratory was the Cavendish experiment conducted by the British scientist Henry Cavendish in 1798. It took place 111 years after the publication of Newton's Principia and approximately 71 years after his death. |
Newton's Three Laws of Motion
Newton's laws of motion are three physical laws that, together, laid the foundation for classical mechanics. They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces. More precisely, the first law defines the force qualitatively, the second law offers a quantitative measure of the force, and the third asserts that a single isolated force doesn't exist. These three laws have been expressed in several ways, over nearly three centuries, and can be summarized as follows:
- First law: In an inertial frame of reference, an object either
remains at rest or continues to move at a constant velocity,
unless acted upon by a force.
- Second law:In an inertial reference frame, the vector sum of
the forces F on an object is equal to the mass m of that object
multiplied by the acceleration a of the object: F = ma.
- Third law:When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
The three laws of motion were first compiled by Isaac Newton in his Philosophić Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), first published in 1687. Newton used them to explain and investigate the motion of many physical objects and systems. For example, in the third volume of the text, Newton showed that these laws of motion, combined with his law of universal gravitation, explained Kepler's laws of planetary motion.
Calculus
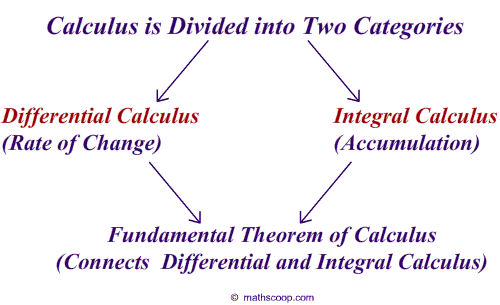 |
Calculus (from Latin calculus, literally 'small pebble', used for counting and calculations, as on an abacus) is the mathematical study of continuous change, in the same way that geometry is the study of shape and algebra is the study of generalizations of arithmetic operations. It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under and between curves). These two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergence of infinite sequences and infinite series to a well-defined limit. Generally, modern calculus is considered to have been developed in the 17th century by Isaac Newton and Gottfried Wilhelm Leibniz. Today, calculus has widespread uses in science, engineering, and economics. Calculus is a part of modern mathematics education. A course in calculus is a gateway to other, more advanced courses in mathematics devoted to the study of functions and limits, broadly called mathematical analysis. Calculus has historically been called "the calculus of infinitesimals", or "infinitesimal calculus". The term calculus (plural calculi) is also used for naming specific methods of calculation or notation as well as some theories, such as propositional calculus, Ricci calculus, calculus of variations, lambda calculus, and process calculus. Gottfried Leibniz (a brilliant mathematician and Natural Philosopher from Germany) independently discovered Calculus two decades after Newton had developed his Fluxions (his version of Calculus). Newton kept his Fluxion’s secret, as was his nature, but Leibniz published his Calculus. Although the Newtonian notations and name of Fluxions were difficult to utilize, the methods of Newton were superior to Leibniz. Therefore, mathematicians and scientists adopted the methods of Newton, but the name and notations of Leibniz.
|
Space as a Rubik’s Cube and Linear Time
Newton envisions space and time as four-dimensional. Each piece of space had a fixed length, width, and height (as three dimensions), and time (as the fourth dimension) which move linear (from past to present to future) at a constant rate such as a metronome (tick-tock, tick-tock, tick-tock, tick-tock).
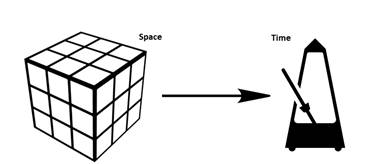
This view of the universe would be replaced by Einstein’s Special Theory of Relativity, which interrelated space and time into spacetime, and made space flexible and time variable (relative spacetime).
Newton’s Character
To say that Newton was an eccentric character is an understatement. He was an egotistical egomaniac, highly suspicious and secretive to the point of paranoia. He knew he was the greatest scientist of his time, and he expected all others to acknowledge his greatness. He would also brook no criticism or critique of his theories and was totally dismissive of all scientific theories with which he disagreed. Easy to offend, Newton was very vindictive to all who offended him. Newton had many confrontations, with both scientist and others, in which his difficult personality led to many problems. Although Newton was the greatest scientist who ever lived, he may also be the greatest pain-in-the-ass scientist that ever lived, although many other scientists throughout history were jockeying for this dubious honor. Here are some personal stories about him.
When Newton was born it was expected that he would not survive. He was underweight and had a sickly appearance, and all were expecting him to pass away within a few days. But he survived and grew up to be the greatest scientist that ever lived. However, he had numerous character flaws due to his upbringing. Several months before Newton was born his father died and he was raised by his single mother and his mother’s parents. Although Newton's father was not rich he did have a small estate and the family was not want for food and lodging. Several years later Newton’s mother remarried a more prosperous man. Newton was not adopted by his mothers’ new husband, and Isaac and his mother’s new husband intensely disliked each other. So much so that Newton was sent back to his maternal grandparents to be raised. His maternal grandparents were not that fond of Isaac, but they did get along enough to raise Isaac. As Isaac was a somewhat smaller and robust boy he was not involved in playing with boys of his age. Indeed, the other boys did not like him because Newton was so smart he would point out all the stupidities of the other boys. This led to constant teasing of Isaac Newton, although sometimes Newton was helpful to the other boys. Newton did have a few female friends, but these were of no consequence in his upbringing. Indeed, Newton became a lifelong bachelor and was never known to have any romantic interest or sexual relationships with woman (or men).
Newton's intelligence was very noticeable, as well as his disinclination to get involved in anything other than his observations, studies, and model making of mechanical contrivances. The attempts of Newton's mother's husband to get Newton involved in the business of farming we’re also a disaster. With the assistance of some influential people, Newton was admitted to Cambridge University to pursue a religious and academic career. Newton's undergraduate years at Cambridge University we're somewhat difficult. Newton had an inheritance from his natural father, and his mother's husband was a prosperous farmer. However, Newton's mother would not spend any of Newton’s inheritance on his academic needs, not to mention her husband wanted nothing to do with Isaac. Therefore, Isaac had to do menial work at Cambridge to support his academic needs. It was also a time at Cambridge in which there was practically no academic supervision, and Newton was free to pursue his studies on whatever he was interested in. Mathematics and science were his interest, but Cambridge did not have much in the way to offer in these subjects. However, Cambridge had a good library and Newton extensively used the library to gain his knowledge in these fields. The newly-created Lucasian Chair of Mathematics was filled by the professor who had the most knowledge and experience in mathematics. He took a shine to Newton and recognize Newton's genius in mathematics. He tutored Newton in mathematics as much as he could, but he soon realized that Newton’s abilities were greater than his own abilities. He was politically connected and used his influence to assure that Newton got his degree and was hired by Cambridge, in what we now known as a graduate position. When he decided to vacate the chair to pursue other personal goals he recommended and pushed for Newton to be named the Lucasian Professor of Mathematics. Newton was appointed to this position and served for over 40 years as Lucasian Professor of Mathematics at Cambridge.
Because of Isaac's circumstances and upbringing, he developed many unpleasant characteristics. He was a loner lacking in social graces. To say that he did not suffer fools gladly was an understatement, as he told people he thought were foolish to go away as they did not know what they were talking about. He was also very paranoid and suspicious of the motives of all those around him. He was concerned that others would steal his ideas and work then take credit for them, a very common occurrence in Newton’s time. As a result, he did not often share or publish his findings, but those that he did share and publish where recognized as works of genius. Newton was also a vindictive person, and if you crossed him he often set out to destroy you and often succeeded. The Natural Philosopher Robert Hooke was often a target of Newton's vindictiveness, as Hooke had a very bad habit of claiming that he had he had already made the discovery when another scientist announced their discoveries. He tried this several times with Newton’s discoveries and Newton set out to discredit him, which he did. When Gottfried Leibniz (a brilliant mathematician and scientist from Germany) independently discovered Calculus decades after Newton had developed his Fluxions (his version of Calculus) Newton discovered that Leibowitz had read a short paper that Newton had written giving a brief outline of the method of Fluxions. Newton then claimed that Leibniz had stolen his ideas and set out to destroy Leibniz in order to maintain his priority of discovery. A bitter scientific war of words and letters broke out between the English who defended Newton, and the Germans and other Europeans who defended Leibniz. It didn’t help Leibniz that he lied about reading the short paper, and therefore Newton was able to discredit Leibniz. The bitterness of that argument lasted for many decades after both he and Leibniz had died.
Newton had other peculiarities that in today’s world would seem odd, but in his time were not considered out of the ordinary; Alchemy and Biblical Interpretation. Alchemy in Newton’s time was much more than the quest to turn base metals into gold. Indeed, those alchemist that engaged in turning metals into gold were looked down upon by the other alchemist, who was trying to figure out the nature of the base metals and how they worked. Newton had no interest in turning anything into gold, but he was very interested in discovering how things worked. Newton was deeply interested in all forms of natural sciences and materials science, an interest which would ultimately lead to some of his better-known contributions to science.
During Newton's lifetime, the study of chemistry was still in its infancy, so many of his experimental studies used esoteric language and vague terminology more typically associated with alchemy and occultism. It was not until several decades after Newton's death that experiments of chemistry under the pioneering works of Antoine Lavoisier were conducted, and analytical chemistry, with its associated nomenclature, came to resemble modern chemistry as we know it today. However, Newton's contemporary and fellow Royal Society member, Robert Boyle, had already discovered the basic concepts of modern chemistry and began establishing modern norms of experimental practice and communication in chemistry, information which Newton did not use. Recently, many new papers on Newton’s efforts in alchemy were discovered, and scholars realized that Newton efforts were as much chemistry as it was alchemy. Unfortunately, his Alchemy experiments led to no insights that were useful for Chemistry.
Newton was also a committed believer in God and the Bible, but not of the religious doctrine of the Church. He expended much effort into reading and trying to interpret the underlying meaning of the Bible, looking for hidden insights on nature in the Bible. In reviewing Newton’s notes and papers on the Bible modern scholars can confidently say that Newton’s work on this subject was complete nonsense.
James Clerk Maxwell
 |
James Clerk Maxwell (Scottish: 13 June 1831 – 5 November 1879) was a scientist in the field of mathematical physics. His most notable achievement was to formulate the classical theory of electromagnetic radiation, bringing together for the first time electricity, magnetism, and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the "second great unification in physics" after the first one realised by Isaac Newton. With the publication of "a dynamical theory of the electromagnetic field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. Maxwell proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. The unification of light and electrical phenomena led to the prediction of the existence of radio waves. Maxwell helped develop the Maxwell–Boltzmann distribution, a statistical means of describing aspects of the kinetic theory of gases. He is also known for presenting the first durable colour photograph in 1861 and for his foundational work on analyzing the rigidity of rod-and-joint frameworks (trusses) like those in many bridges. His discoveries helped usher in the era of modern physics, laying the foundation for such fields as special relativity and quantum mechanics. Many physicists regard Maxwell as the 19th-century scientist having the greatest influence on 20th-century physics. His contributions to the science are considered by many to be of the same magnitude as those of Isaac Newton and Albert Einstein. In the millennium poll – a survey of the 100 most prominent physicists – Maxwell was voted the third greatest physicist of all time, behind only Newton and Einstein. On the centenary of Maxwell’s birthday, Einstein described Maxwell’s work as the "most profound and the most fruitful that physics has experienced since the time of Newton".
|
James Clerk Maxwell was considered the Newton of his time. Every physicist (to this day) have immense respect for him and his work. Every physicist of his time consulted with Maxwell to obtain his advice, opinion, and insight. Maxwell took James Faraday’s experimental results on magnetism and electricity and created the Theory of Electromagnetism.
It was with his Theory of Electromagnetism that Maxwell contributes to Gravity. In Newtons’ gradational theory and laws of motion, the speed of an object was dependent on many factors. For instance, if you were on a train moving at 50 mph, and you shot a bullet in the direction of the movement of the train (the average bullet travels at around 1,700 mph), an observer standing outside of the train would measure the bullets speed as 1,750 mph. The speed of the train would be added to the speed of the bullet to determine the final speed of the bullet. Depending on which direction you shot the bullet an outside observer would measure the bullet speed by cumulating (+ or -) all these factors.
However, Maxwell proved that the speed of light was absolute (never varied) at approximately 186,000 mph. So, if you were on any moving object and released a light beam an outside observer would measure the speed of the light beam of 186,000 mph. No matter which direction the light beam was pointed, or the speed of the object from which you fired the light beam, the speed of light did not change (it was not cumulative).
This and other electromagnetic experiments that differed from Newton raised troubling questions as to the correctness of Newton’s Universal Gravity and Laws of Motion. Questions that Albert Einstein would answer. The Theory of Electromagnetism was the basis for Einstein’s Theory of Special Relativity and is the only Classical Physics Theory that survived the Quantum Revolution in physics. Even Newton’s theories did not survive (although they are still utilized by engineers of today, but not by physicists).
Maxwell’s Character
James Clerk Maxwell was one of the most boring physicists in history. Although he was a genius there was nothing special about his personal life and character. His ego and personality were such that there were no personality clashes or conflicts with the other scientist of his time. Everybody liked and respected Maxwell and sought out his advice and critiques. There was no controversies or scandals in his personal life, and his marriage appeared to be happy and faithful. He was the smart and wise uncle that everybody wished they had.
Albert Einstein
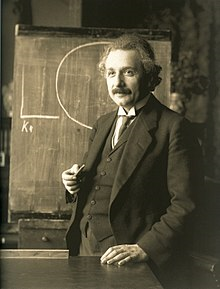 |
Albert Einstein (German born: 14 March 1879 – 18 April 1955) was a theoretical physicist who developed the theory of relativity, one of the two pillars of modern physics (alongside quantum mechanics). His work is also known for its influence on the philosophy of science. He is best known by the general public for his mass–energy equivalence formula e = mc2 (which has been dubbed "the world's most famous equation"). He received the 1921 Nobel Prize in physics "for his services to theoretical physics, and especially for his discovery of the law of the photoelectric effect", a pivotal step in the evolution of quantum theory. Near the beginning of his career, Einstein thought that Newtonian mechanics was no longer enough to reconcile the laws of classical mechanics with the laws of the electromagnetic field. This led him to develop his Special Theory of Relativity during his time at the Swiss patent office in Bern (1902–1909), Switzerland. However, he realized that the principle of relativity could also be extended to gravitational fields and—with his subsequent Theory of Gravitation in 1916—he published a paper on General Relativity. He continued to deal with problems of statistical mechanics and quantum theory, which led to his explanations of particle theory and the motion of molecules. He also investigated the thermal properties of light which laid the foundation of the photon theory of light. In 1917, he applied the General Theory of Relativity to model the large-scale structure of the universe. Between 1895 and 1914, he lived in Switzerland (except for one year in Prague, 1911–12), where he received his academic diploma from the Swiss Federal Polytechnic in Zürich (later the Eidgenössische Technische Hochschule, ETH) in 1900. He later taught at that institute as a professor of theoretical physics between 1912 and 1914 before he left for Berlin. In 1901, after being stateless for more than five years, he acquired Swiss citizenship, which he kept for the rest of his life. In 1905, he was awarded a PhD by the university of Zürich. The same year, his Annus Mirabilis (miracle year), he published four groundbreaking papers, which were to bring him to the notice of the academic world, at the age of 26. He was visiting the United States when Adolf Hitler came to power in 1933 and—being Jewish—did not go back to Germany, where he had been a professor at the Berlin Academy of Sciences. He settled in the United States, becoming an American citizen in 1940. On the eve of World War II, he endorsed a letter to president Franklin D. Roosevelt alerting him to the potential development of "extremely powerful bombs of a new type" and recommending that the U.S. begin similar research. This eventually led to what would become the Manhattan Project. Einstein supported defending the allied forces, but generally denounced the idea of using the newly discovered nuclear fission as a weapon. Later, with the British philosopher Bertrand Russell, he signed the Russell–Einstein manifesto, which highlighted the danger of nuclear weapons. He was affiliated with the Institute for Advanced Study in Princeton, New Jersey, until his death in 1955. Einstein published more than 300 scientific papers along with over 150 non-scientific works. His intellectual achievements and originality have made the word "Einstein" synonymous with "Genius”. |
In my discussion on Einstein I concentrate on his General Theory of Relativity, as it is this theory that deals with Gravity. Einstein’s Special Theory of Relativity deals with the interrelationship of space and time now referred to as spacetime and the linear (straight line) motion of bodies. Special relativity implies a wide range of consequences, which have been experimentally verified, including length contraction, time dilation, relativistic mass, mass-energy equivalence, a universal speed limit and relativity of simultaneity. It also contains his famous formula E=mc2. Special Relativity is only indirectly related to Gravity and is therefore not apropos to this article on Gravity. However, Special Relativity is incorporated into General Relativity as a special case and is not invariant with General Relativity.
An Outline of Einstein’s Life
I shall discuss Einstein’s contribution to Gravity by presenting a brief outline of the life of Albert Einstein that highlights his means, methods, and achievements.
Childhood
Albert Einstein was born into a middle-class family whose father and Uncle owned an electrical business together. Their business was mainly in the manufacture of electrical generators and electrical motors. Although Albert was initially thought to be slow, because of his unwillingness to speak, it soon became apparent that he was actually a very bright child. His parents encouraged his education and intellect, and as soon as he was old enough they allowed him to play in the research laboratory of his fathers and uncles business. He recalled that time as being a very happy time in his life, and he was able to do and see many interesting things in the laboratory. He was especially fond of a compass that his father a given him, and he was fascinated by the fact that no matter where he carried this compass it would always point to the North Pole. This spurred his interest in physics and mathematics in which he excelled. He was always asking questions about why and how things worked. One of the questions that he asked himself during this time, and which there was no answer, was if he could run alongside a beam of light what the world would look like to him. This question stayed with him throughout his young life, and the answer to this question would be one of his greatest scientific discoveries.
University Years
In 1895, at the age of 16, Einstein took the entrance examinations for the Swiss Federal Polytechnic in Zürich (later the Eidgenössische Technische Hochschule - ETH). He failed to reach the required standard in the general part of the examination but obtained exceptional grades in physics and mathematics. On the advice of the principal of the Polytechnic, he attended the Argovian Cantonal school (gymnasium) in Aarau, Switzerland in 1895 and 1896 to complete his secondary schooling. In September 1896, he passed the exams with good grades including on a scale of 1–6, a top grade of 6 in physics and mathematical subjects. At 17, he enrolled in the four-year mathematics and physics teaching diploma program at the Zürich Polytechnic.
During his Zürich Polytechnic student years, Einstein made a few good friends, Michele Angelo Besso, Marcel Grossmann, Friedrich Adler, and Mileva Maric (with whom he married in 1903). He remained good friends with all of them (except Mileva Maric) throughout their lifetimes.
Einstein was a very poor student at the University, not because of his intellect or abilities, but because he would not behave as a student was expected. In Germany, in Einstein's time, a student was expected to show up for a lecture and which the student would carefully listen to the professor, take good notes, and only ask a question to help clarify what the professor had said. But Einstein was always challenging what the professor said, and this made him very unpopular with the professors. It became so bad that many of his professors made it clear to Einstein that they did not wish him to attend their lectures. Instead, Einstein often sat around a coffee table with his friends and discuss the latest papers and experiments in physics, and they would argue as to their meaning. Einstein found this very stimulating, as it forced him to think and consider his friend's thoughts on the papers and experiments.
This became a problem for Einstein when he was about to graduate. In order to receive his University degree, he had to pass a final exam, an exam which was on what the professors had lectured, which he had not attended. Fortunately, Einstein's friend Marcel Grossmann had attended the lectures and was an excellent note keeper. Einstein borrowed his friend's notes and studiously study them for the next two weeks. He passed the exam with flying colors and then said he promptly forgot everything he had studied in the previous two weeks because he knew it was incorrect.
His next problem was in obtaining employment as a University teacher or research assistant. In Germany at that time, the way you obtained these positions was through a recommendation by your professor, and Einstein could not obtain any recommendations by any of his professors as they disliked him. He was therefore unable to obtain a job in his chosen profession. However, his uncle and Marcel Grossmann father were able to obtain a job for Einstein in the Bern Switzerland Patent Office. As Einstein was newly married and had a child with another on the way he accepted this job to support his family. This unfortunate circumstance, however, turned out to be one of the best things that could have happened to him.
Patent Clerk
His position (Patent Clerk 2nd class) at the Swiss patent office in Bern Switzerland (from 1902–1909), required him to punctually show up for work where a stack of patent applications was waiting on his desk for him to review. He was responsible for reviewing the patent applications for any scientific problems or inconsistencies, and if he found any problems or inconsistencies the patent application was rejected. Otherwise, it was passed on to the Patent Clerk (1st class) who reviewed the application to determine if another patent conflicted with it. He was so good at this job that it only took him a few hours to go through the stack of patent applications that was assigned to him. He, therefore, worked on a few of the patent applications, then paused to read physics journals and think about what he had read. He would then review a few more patent applications, pause, and read and think ad infinitum throughout the day. This allowed Einstein plenty of time to keep current or what was happening in the world of physics. In 1904 he started concentrating on three subjects concerning physics; the existence of atoms, the photoelectric effect, and special relativity. In 1905 he had his “Annus Mirabilis” (Miracle Year), in which he published four papers on these three subjects (and a fifth paper in 1906), which resolved these subjects.
The first the first of these subjects had to do with the existence of atoms and molecules. One day Einstein was having a cup of tea in which he placed a lump of sugar. He examined how the sugar dissolved in the tea and postulated that it was a result of the collisions between atoms and molecules, which at that time had not been proven to exist. He abstracted the experiment to deal with pure hot water (a simple molecule), and a pure cold crystal. He was then able to show, mathematically, the motion was a result of the diffusion of an object at a particular rate (known as the mean squared displacement), and that this rate depended upon the number of atoms or molecules in a mole of the fluid in which the object is suspended (Avogadro’s number). From this one could determine the size of molecules or atoms. For the first time, a measurable quantity allowed us to probe the atomic realm. It wasn’t just the idea, but rather the precision of Einstein’s results that many scientists found so convincing. Utilizing his mathematics along with experimentation it was possible to determine the sizes and masses of atoms and molecules.
The second subject had to do with the photoelectric effect. The photoelectric effect refers to the emission, or ejection, of electrons from the surface of, generally, a metal in response to incident light. Max Planck at the end of the 1890’s had postulated the existence of energy quanta as the reason for Black Body Radiation, but his explanation had several unresolved problems (mainly the Photoelectric Effect and the Ultraviolet Catastrophe). There was also the problem that in most experiments light generally behaved as a wave, but in some experiments, light was behaving as if it were a particle. Also, Planck did not believe that quanta actually existed, but we're only a mathematical trick to explain the phenomena. Albert Einstein, however, believed they actually existed, and that light was much stranger than anyone had imagined. Einstein showed that light had a dual nature – sometimes it behaved as a wave, and sometimes it behaved as a particle. Depending on the experiment you were conducting you were either measuring the wave nature of light or the particle nature of light. He described light as composed of discrete quanta (now called photons) as opposed to continuous waves, but that light traveled in a wave-like manner and interacted with other matter in a particle fashion. This explanation resolved all the problems and discrepancies of Black Body Radiation, the Photoelectric Effect, and the Ultraviolet Catastrophe. It was for this theory that Einstein was awarded his only Nobel Prize in 1921.
The third subject had to do with his question, as a young man, of what the world would look like if you could run next to a beam of light. Einstein was very punctual in arriving at the patent office, as was required at that time. He took the same trolley every day, at the same time, from his apartment to the patent office, and he even sat in the same seat each day. As this trolley pass by the Town Center on the way to the patent office, Einstein was looking forward in his trolley ride to the center of town, and he often looked at the clock tower. After passing the Clock Tower he would start looking at the patent office and think about what he was going to read that day. One day, due to a family issue, he missed his regular trolley and had to catch the next trolley. This time he was facing away from the Clock Tower when he approached the town center, and when he passed the Clock Tower he was facing the clock. He began to wonder what's a clock would show if he was riding on a beam of light instead of a trolley. He realized that as he traveled faster and faster it would take the next beam of light, that showed the next minute, longer to overtake the beam of light he was traveling on and therefore the clock would appear to run slower. He also realized that if he was traveling at the speed of light the next beam of light would never overtake him, and for all intents and purposes, time stood still for a beam of light. He then looked over his shoulders and realized he was traveling so fast that everything to the right and left of him looked foreshorten. He then looked over his back and realized that the entire universe would slowly collapse in front of him as he was traveling toward the speed of light, eventually into a single point in the direction of travel when he reached the speed of light. He also realized that as he was traveling faster toward the speed of light that it would take more and more energy to speed him up, and that it would take all the energy in the universe to get him to the speed of light. This meant that mass could never be accelerated to the speed of light. This was an astounding insight and Einstein was very excited about it. He rushed to his desk in the patent office and immediately went through a stack of patent applications, and then stopped reviewing the patent applications and started doing the mathematics of his insight. By noon he had the answer mathematically and scientifically, and he stated it was one of the most exhilarating moments of his life that he knew something about the universe that no one else knew. Upon further work on this Insight, he realized that not only did Time, Length, and Mass change relative to your speed, but that different observers at different places traveling at different speeds could look at the same phenomena and report back different observations of what they had seen because of this effect. He named this phenomenon Relativity (which we now know as Special Relativity to distinguish it from General Relativity, which he developed a few years later). His science and math were based on Maxwell’s equations of electrodynamics, and Maxwell's equations were one of the few things that survived from classical physics because of this. He also realized that as a result of this phenomena mass and energy were equivalent, which resulted in his famous equation: E=mc2.
Einstein would continue to publish papers on the impacts of his insights, but he was generally ignored. After all, who could take seriously an unknown, unaffiliated, physicist from Bern Switzerland (he took pains to hide his occupation as a patent clerk)? Max Planck, however, took an interest in his Special Relativity and other prominent physicist started reviewing his work. In 1907 several light experiments were performed in which only Einstein’s Photoelectric Theory could explain the results. More physicist started taking him seriously, and by 1909 it was recognized that he was a genius (which allowed him to leave the patent office and become an associate professor of Theoretical Physicist at the University of Zürich). His previous papers were then studied and incorporated into the new field of Quantum Physics, and it is generally recognized that his “Annus Mirabilis” was the pivotal year in the break between Classical and Modern Physics.
Theoretical Physicist
By 1908, Einstein was recognized as a leading scientist and was appointed lecturer at the University of Bern in Switzerland. The following year, after giving a lecture on electrodynamics and the relativity principle at the University of Zürich in Switzerland, he was recommended to the faculty at the University of Zürich for a newly created professorship in theoretical physics. Einstein was appointed an associate professor in 1909, and Einstein became a full professor at the German Charles-Ferdinand University in Prague Czechoslovakia in April 1911. Thereafter, he held several positions as a Theoretical Physicist at notable institutions throughout Europe and the United States. By the time Einstein became a Theoretical Professor, he had become interested in the problem of Gravity. Newton’s Theory of Universal Gravity had held sway for over two hundred years, but it never explained what gravity was, only how it worked (a point that Newton freely acknowledged). In addition, there were also some cracks that were beginning to appear with Newtonian gravity (mainly the Precession of the Perihelion of Mercury’s orbit). Einstein spent the next several years working on gravity (a period that he called the most arduous of his life). As a result of these efforts, he formulated the Theory of General Relativity which explained all of gravity, and which also incorporated his Special Relativity theory. General Relativity has since withstood all observations and experiments to become a bedrock of modern physics.
His great insight in 1907 was that gravity and acceleration behaved in the same manner. He imagined that if you were in a sealed box in deep space, with no gravity present, you would be floating in the box with no sense of gravity. If, however, you started the box moving in a linear motion you would start to feel gravity in the opposite direction of the linear motion. And the faster the box moved the more gravity you would feel. Therefore, acceleration caused a gravitational effect, and therefore gravity was caused by acceleration. He also realized that light would “bend” in an accelerating box. This is known as the Principle of Equivalence as illustrated below.
The Equivalence Principle
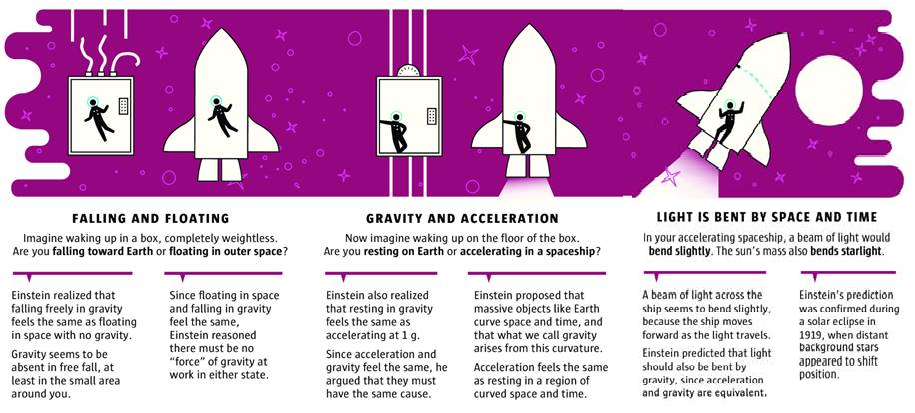
Geometric Mathematics
If light is bent, it must because it is traveling on a curved surface. Since ancient times Euclidian (Plain) geometry was understood to apply to flat surfaces. In more modern times it was discovered that curved surfaces had a Non-Euclidian (Spherical) geometry. The best example is how parallel lines behave on a plane or spherical surface as illustrated below.
 Plane (Flat) Geometry of Parallel Lines |
 Spherical (Curved) Geometry of Parallel Lines |
On a plane surface, two parallel lines can never meet. But imagine on a globe of the earth (which is spherical) two parallel lines are drawn at the equator. As they go up (or down) the globe the curvature of the Earth bends the lines until they meet at the north (or south) pole. Continuing these lines after they cross over each other at the poles and they will become parallel lines when they intersect the equator.
Einstein, therefore, reasoned that as light was being bent that meant that light, and therefore gravity, is working on a curved surface. Einstein also realized that as gravity was not constant (it became greater that more you accelerated) it was not truly spherical. It was more like different size hills and valleys, and he needed a mathematics that could describe this geometry. As he was unaware of any mathematics that could do this, so he contacted a University friend who was a mathematician to describe his problem to him. His friend, Marcel Grossmann, informed Einstein of Riemannian geometry which was the mathematics he needed. Einstein asked if he knew anybody who could tutor him in Riemannian geometry (as it was a rare mathematical disciple, and exceedingly difficult). Marcel Grossmann informed Einstein that he was one of the few experts in Riemannian geometry and that he could tutor him. For the next two years Marcel Grossmann taught Einstein Riemannian geometry. Einstein was often quoted as saying that these two years were the most difficult years of his professional life. However, Einstein was able to master Riemannian geometry and utilize it to develop his Theory of General Relativity which explained Gravity. Einstein utilized Riemannian geometry to develop his field equations (Einstein’s Field Equations - EFE; also known as Einstein's equations) which comprise a set of 10 equations in the General Theory of Relativity that describe the fundamental interaction of gravitation as a result of spacetime being curved by mass. Einstein published his General Relativity in 1916, to much excitement and skepticism, but five years later he was proven correct by the measurement of the deflection of starlight during a solar eclipse. Newton’s Theory of Gravity was dethroned to be replaced by Einstein’s Theory, and Einstein became a superstar to the general public.
 |
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions. Riemannian geometry was first put forward in generality by Bernhard Riemann in the 19th century. It deals with a broad range of geometries whose metric properties vary from point to point, including the standard types of Non-Euclidean geometry. Any smooth manifold admits a Riemannian metric, which often helps to solve problems of differential topology. It also serves as an entry level for the more complicated structure of pseudo-Riemannian manifolds, which (in four dimensions) are the main objects of the theory of general relativity. Other generalizations of Riemannian geometry include Finsler geometry. |
Einstein eventually returned to Quantum Physics after finishing his General Relativity Theory, but he was dismayed by the course it had taken under Neils Bohr. At that point, he became a critic of Quantum Theory who raised more objections than contributions to Quantum Physics (but his objections were profound and provoked much discussion and reassessment which led to better Quantum Physics).
The last few decades of Einstein’s life were then spent trying to reconcile Quantum Theory and General Relativity, to no avail. We are still, to this day, trying to reconcile Quantum Physics with General Relativity.
Einstein’s Character
If Isaac Newton was the greatest pain-in-the-ass scientists who ever lived than Albert Einstein, with the possible exception of James Clerk Maxwell, was the most beloved scientist in history. Born a German Jew he grew up with a natural dislike of authority and militarism. So much so that he revoked his German citizenship as a young man and became a Swiss citizen. When he moved to the United States to escape Nazism he obtained dual citizenship as an American and Swiss citizen. He was a lifelong pacifist, except when he recognized the existential threat of Nazism and Fascism and supported the American entry into World War II. Upon realizing that the German scientists had the knowledge and capability to construct an atomic bomb he urged President Franklin D. Roosevelt to develop an American atomic bomb. He was appalled when the atomic bomb was used on Japan, and he became a proponent of Nuclear Disarmament. Essentially non-religious in his younger life he became more religious later in life, and he also became a supporter of the Zionists movement. Offered the Presidency of Israel he turned it down, as he knew he would be a disaster as a political leader. Einstein was also an amateur violinist, at which he was not very good, and often used his violin playing to entertain his friends and help him concentrate his thoughts.
During his Polytechnic student years, Einstein made a few good friends, Michele Angelo Besso, Marcel Grossmann and Friedrich Adler, and he remained friends with them throughout their lifetimes. He also utilized these friends’ assistance in developing his scientific theories. During the course of his scientific career, he also made other good friends with whom he remained in contact throughout their lifetimes.
Einstein’s romantic and sexual life was complicated. He had a pre-university romance, a marriage, divorce, and then remarriage. He was known for philandering as his first marriage failed, as well as philandering during his second marriage.
When Einstein was a young man he was considered handsome and a good prospect for marriage. He had a brief relationship with Marie Winteler, a local young lady. He soon broke up with her (who Einstein believed had become clingy) and wrote a letter to her mother explaining his reasoning. In this letter, an 18-year-old Einstein who had been invited to stay at the family’s country house. Einstein declines the invitation, citing that he would not want to lead on young Marie any more than he already has. It is a remarkably discerning and introspective letter, which illustrates not only the emotional and social maturity of Einstein, but also his becoming self-aware that physics is not merely something he wants to do — it is something he must do.
Upon entering the University he met Mileva Maric, and intelligent young physics student, with whom he soon fell in love with. Mileva was not very attractive, but Albert stated that it was her mind that he was most attracted too. The relationship did not have the approval of Albert’s or Mileva’s mother, but they eventually accepted it. They married after Einstein obtained a position at the Swiss Patent Office and he could afford to support both of them. Soon after, Albert and Mileva started a family. Albert's three children were from his relationship with Mileva, his daughter Lieserl being born a year before they married, and who was given up for adoption before the marriage.
Lieserl Einstein (born January 1902 – last mentioned in 1903; possible date of death, 18 September 1903) was the first child of Mileva Maric and Albert Einstein. According to the correspondence between her parents, Lieserl was born in January 1902, a year before her parents married, in Novi Sad, Vojvodina, present-day Serbia, and was cared for by Mileva and her mother for a short time while Einstein worked in Switzerland. When Mileva joined Albert in Switzerland it was without the child, as Lieserl had been given up for adoption to a good friend of Mileva. It was rumored that Lieserl was a sickly child and she died at an early age. Lieserl's existence was unknown to biographers until 1986 when a batch of letters between Albert and Mileva was discovered by Hans Albert Einstein's daughter Evelyn. It is reported (and probably true) that Einstein never saw his daughter.
Hans Albert Einstein (May 14, 1904 – July 26, 1973) was a Swiss-American engineer and educator, the second child and first son of Albert Einstein and Mileva Maric. Hans A. Einstein was a professor of Hydraulic Engineering at the University of California, Berkeley, and was recognized for his research on sediment transport.
Eduard Einstein (28 July 1910 – 25 October 1965) was born in Zürich, Switzerland, the second son of physicist Albert Einstein from his first wife Mileva Maric. Eduard was a good student and had musical talent. After high school, he started to study medicine to become a psychiatrist, but by the age of twenty, he was diagnosed with schizophrenia. He was institutionalized two years later for the first of several times. Biographers of his father have speculated that the drugs and "cures" of the time damaged rather than aided the young Eduard. His brother Hans Albert Einstein believed that his memory and cognitive abilities were damaged by electroconvulsive therapy treatments. After suffering a breakdown, Eduard told his father that he hated him. Albert Einstein emigrated to the United States from Germany in 1933 after the rise of the Nazi German government, and never saw Eduard again. His mother cared for Eduard until she died in 1948. From then on Eduard lived most of the time at the psychiatric clinic Burghölzli in Zurich, where he died of a stroke in 1965 at the age of 55.
It is known that Einstein was a good father to Hans and Eduard during their younger lives. However, the strain of the breakup and divorce with their mother put a strain on his relationships with his sons, and it would be a contentious relationship during this period. Einstein tried to maintain a harmonious relationship with his sons but often failed. During Einstein’s later life Hans and Albert had a reconciliation, but Eduard and Albert never reconciled.
The divorce with Mileva was contentious and somewhat bitter. Mileva never obtained her university diploma (she failed the final exam thrice), and therefore never had a career as a physicist which she had dreamed of since adolescence. As Albert’s fame grew her resentment grew and this put a great strain on their marriage. The loss of their daughter Lieserl also played a part in the dissolving marriage. Einstein was also a difficult man to live with. He often brought his work home with him. When he did this, he demanded quiet and no interruptions of his thoughts or calculations. He was also not interested in the day-to-day activities of running a household. He expected that Mileva would handle all these responsibilities. Then, as the marriage began to dissolved Einstein started philandering with his secretary followed by his cousin Elsa. At this point, the marriage was effectively over. The divorce took several years to finalize with contentious negotiations on the financial support for Mileva and Einstein’s sons.
After his divorce from Mileva, Albert realized he needed a wife to take care of his earthly needs as he pursued his scientific endeavors. His cousin Elsa Einstein (with whom he started having sexual trysts) was always smitten with Albert, and she gladly stepped into this role. They were affectionate with each other, but probably not in love, but they decided to marry. As Albert was gaining fame in the physics world he had the opportunity, and took advantage of it, to engage in sexual trysts with many adoring women. After gaining world fame the opportunities to philander became much greater to which Albert indulged himself. As long as the relationship was not serious Elsa didn’t seem to mind, as she was enthralled at being the wife of the great Albert Einstein. There was also the social status, wealth, security and travel of being Albert Einstein’s wife.
For her reasons, Elsa stayed with Einstein despite his flaws and explained her views about him in a letter: "Such a genius should be irreproachable in every respect. But nature does not behave this way, where she gives extravagantly, she takes away extravagantly."
But it's not to say Einstein didn't have a conscience about his personal failures. Writing to a young gentleman, Einstein admitted as much; "What I admire in your father is that, for his whole life, he stayed with only one woman. This is a project in which I grossly failed, twice."
For all of Einstein's immortalized genius, his love life proved he was very much a human tethered to Earth.
Albert Einstein Quotes:
Albert Einstein was one of the most quotable scientists, not only on science but life itself. Below are some of my favorite Einstein quotes.
|
“A man should look for what is, and not for what he thinks should be.” “All that is valuable in human society depends upon the opportunity for development accorded the individual.” “Any man who reads too much and uses his own brain too little falls into lazy habits of thinking.” “Anyone who has never made a mistake has never tried anything new.” “Common sense is nothing more than a deposit of prejudices laid down by the mind before you reach eighteen.” “Do not worry about your difficulties in mathematics, I can assure you that mine are all greater.” “Education is what remains after one has forgotten what one has learned in school.” “Falling in love is not at all the most stupid thing that people do— but gravitation cannot be held responsible for it.” “Great spirits have always encountered violent opposition from mediocre minds. The mediocre mind is incapable of understanding the man who refuses to bow blindly to conventional prejudices and chooses instead to express his opinions courageously and honestly.” “Human knowledge and skills alone cannot lead humanity to a happy and dignified life. Humanity has every reason to place the proclaimers of high moral standards and values above the discoverers of objective truth.” “I have no special talent. I am only passionately curious.” “I speak to everyone in the same way, whether he is the garbage man or the president of the university.” “I think and think for months and years. Ninety-nine times, the conclusion is false. The hundredth time I am right.” “I very rarely think in words at all. A thought comes, and I may try to express it in words afterwards.” “I, at any rate, am convinced that He (God) does not throw dice.” “If you can't explain it simply, you don't understand it well enough.” “Imagination is everything. It is the preview of life's coming attractions.” “Imagination is more important than knowledge. For knowledge is limited, whereas imagination embraces the entire world, stimulating progress, giving birth to evolution.” “In order to form an immaculate member of a flock of sheep, one must, above all, be a sheep.” “Information is not knowledge.” “Insanity: doing the same thing over and over again and expecting different results.” “It is the supreme art of the teacher to awaken joy in creative expression and knowledge.” “It's not that I'm so smart, it's just that I stay with problems longer.” “Learn from yesterday, live for today, hope for tomorrow. The important thing is not to stop questioning.” “Life is like riding a bicycle. To keep your balance you must keep moving.” “Memory is deceptive because it is colored by today's events.” |
“No amount of experimentation can ever prove me right; a single experiment can prove me wrong.” “Once we accept our limits, we go beyond them.” “Only a life lived for others is a life worthwhile.” “Pure mathematics is, in its way, the poetry of logical ideas.” “Reality is merely an illusion, albeit a very persistent one.” “Science without religion is lame, religion without science is blind.” “Small is the number of people who see with their eyes and think with their minds.” “The difference between genius and stupidity is that genius has its limits.” “The important thing is not to stop questioning. Curiosity has its own reason for existing.” “The monotony and solitude of a quiet life stimulates the creative mind.” “The most beautiful experience we can have is the mysterious. It is the fundamental emotion that stands at the cradle of true art and true science.” “The most incomprehensible thing about the world is that it is comprehensible.” “The only source of knowledge is experience.” “The only way to escape the corruptible effect of praise is to go on working.” “The secret to creativity is knowing how to hide your sources.” “The true sign of intelligence is not knowledge but imagination.” “The value of a man should be seen in what he gives and not in what he is able to receive.” “To punish me for my contempt for authority, fate made me an authority myself.” “To raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advance in science.” “Truth is what stands the test of experience.” “Try not to become a man of success, but rather try to become a man of value. “ “Two things are infinite: the universe and human stupidity; and I'm not sure about the universe.” “We cannot solve our problems with the same thinking we used when we created them.” “Weakness of attitude becomes weakness of character.” “Whoever is careless with the truth in small matters cannot be trusted with important matters.” “You ask me if I keep a notebook to record my great ideas. I've only ever had one.” |
Some of the Consequences of General Relativity
When scientist started utilizing the field equations of General Relativity they began to predict cosmological phenomena that were totally unexpected or previously unseen. These cosmological phenomena have now been proven to exist and are the proofs of General Relativity. A Wikipedia article on the Tests of General Relativity serve to establish observational evidence for the theory of general relativity. Some of the biggest predicted cosmological phenomena are as follows:
Precession of the Perihelion of Mercury’s Orbit
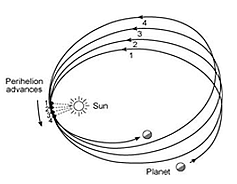 |
A long-standing problem in the study of the Solar System was that the orbit of Mercury did not behave as required by Newton's equations. This problem became observable in the 19th century as advancements in telescopes and measuring instruments made it possible to accurately measure the precession. The problem is that as Mercury orbits the Sun it follows an ellipse...but only approximately. It was found that the point of closest approach of Mercury to the sun does not always occur at the same place in space, but that it slowly moves forward in Mercury’s orbit. This effect is known as precession. The anomalous rate of precession of the perihelion of Mercury's orbit was first recognized in 1859 as a problem in celestial mechanics. |
The precession of the orbit is not peculiar to Mercury, all the planetary orbits precess. In fact, Newton's theory predicts these effects, as being produced by the gravitational attraction of the planets on one another. The precession of the orbits of all planets except for Mercury's can, in fact, be understood using Newton’s equations. But Mercury seemed to be an exception.
As seen from Earth the precession of Mercury's orbit is measured to be 5600 seconds of arc per century (one second of arc=1/3600 degrees). Newton's equations, taking into account all the gravitational effects from the other planets (as well as a very slight deformation of the sun due to its rotation) and the fact that the Earth is not an inertial frame of reference, predicts a precession of 5557 seconds of arc per century. But the actual measurements showed there is a discrepancy of 43 seconds of arc per century from Newton’s predictions.
This discrepancy cannot be accounted for using Newton's formalism. Many ad-hoc fixes were devised to explain this discrepancy. One explanation was that an undiscovered planet orbited between the Sun and Mercury, causing the perturbation of Mercury’s orbit which showed up as precession. The race was then on for astronomers to discover this planet. This supposed planet was even given the name “Vulcan”. A few astronomers actually claimed that they have discovered Vulcan, but it was determined that the discoveries were equipment anomaly’s, observational errors, or very small, long duration sunspots. No astronomer ever discovered Vulcan for the simple fact that it did not exist.
When Einstein developed his Theory of General Relativity he applied it to the problem of Mercury’s Orbit. Einstein was able to predict, without any adjustments whatsoever, that the exact orbit of Mercury is correctly predicted by the General Theory of Relativity. When he did this Einstein realized that General Relativity was correct. However, he required an additional observation of phenomena that Newton’s Universal Gravitation had no allowance for in order to prove his General Relativity was correct. He found this in his prediction of the Deflection of Starlight.
Deflection of Starlight
The first observation of light deflection was performed by noting the change in position of stars as they passed near the Sun on the celestial sphere. The observations were performed by Arthur Eddington and his collaborators during the total solar eclipse of May 29, 1919, when the stars near the Sun (at that time in the constellation Taurus) could be observed. Observations were made simultaneously in the cities of Sobral, Ceará, Brazil and in Săo Tomé and Príncipe on the west coast of Africa. The result was considered spectacular news and made the front page of most major newspapers. It made Einstein and his theory of general relativity world-famous. When asked by his assistant what his reaction would have been if general relativity had not been confirmed by Eddington and Dyson in 1919, Einstein famously made the quip: "Then I would feel sorry for the dear Lord. The theory is correct anyway." The early accuracy, however, was poor. The results were argued by some to have been plagued by systematic error and possibly confirmation bias, although modern reanalysis of the dataset suggests that Eddington's analysis was accurate. The measurement was repeated by a team from the Lick Observatory in the 1922 eclipse, with results that agreed with the 1919 results and has been repeated several times since, most notably in 1953 by Yerkes Observatory astronomers and in 1973 by a team from the University of Texas. Considerable uncertainty remained in these measurements for almost fifty years, until observations started being made at radio frequencies. |
When Einstein first made his prediction on the amount of Deflection of Starlight he made an arithmetical error which gave an incorrect value. As soon as he discovered this error he issued an addendum correcting this mistake.
Several attempts were made to measure the deflection of starlight during a solar eclipse after Einstein’s made his prediction. However, World War I intervened on several of these attempts. The other attempts had transportation, equipment failure, or bad weather preventing a successful observation.
Sir Arthur Stanley Eddington OM FRS (28 December 1882 – 22 November 1944) was an English astronomer, physicist, and mathematician of the early 20th century who did his greatest work in astrophysics. William Wallace Campbell (April 11, 1862 – June 14, 1938) was an American astronomer and director of Lick Observatory from 1901 to 1930. Both Eddington and Campbell made successful observations on the Deflection of Starlight during the 1919 solar eclipse. Both were in a friendly rivalry to be the first to prove or disprove Einstein’s General Relativity through the deflection of starlight. Campbell did some preliminary measurement that showed no deflection of starlight (disproving Einstein) and sent his preliminary results to Eddington. When Eddington received these results he was dismayed, as his preliminary results showed a deflection of starlight (proving Einstein). In reviewing Campbell’s results Eddington noticed a systemic measurement error which had led Campbell astray. Eddington sent his systemic error finding back to Campbell for confirmation. On the day that Eddington was to make his announcement on his results to the Royal Society rumors were rife that Eddington would confirm Einstein and Campbell would refute Einstein. That afternoon Eddington received a telegram from Campbell admitting his initial measurement was indeed incorrect, and his remeasurement confirmed the deflection of starlight as Einstein predicted. Under a large portrait of Isaac Newton in the Royal Society hall Eddington made his announcement to the Royal Society (to the largest audience ever present at a meeting) confirming Einstein, and then read the telegram from Campbell confirming Einstein. A riotous applause erupted, and Newton’s Universal Gravitation was dethroned by Einstein’s General Relativity. Einstein had become a super celebrity outside of the Physics world at that moment.

p.s. Einstein was not present at the Royal Society meeting, as Germans were not allowed to travel outside of Germany for several years after World War I.
Gravitational Redshift of Light
 |
The gravitational redshift of a light wave as it moves upwards against a gravitational field (caused by the yellow star below). Einstein predicted the gravitational redshift of light from the equivalence principle in 1907, and it was predicted that this effect might be measured in the spectral lines of a white dwarf star, which has a very high gravitational field. Initial attempts to measure the gravitational redshift of the spectrum of Sirius-B, were done by Walter Sydney Adams in 1925, but the result was criticized as being unusable due to the contamination from light from the (much brighter) primary star, Sirius. The first accurate measurement of the gravitational redshift of a white dwarf was done by Popper in 1954, measuring a 21 km/s gravitational redshift of 40 Eridani B. The redshift of Sirius B was finally measured by Greenstein et al. in 1971, obtaining the value for the gravitational redshift of 89±16 km/s, with more accurate measurements by the Hubble Space Telescope showing 80.4±4.8 km/s. |
The Curvature of Spacetime
Einstein’s general relativity states that the presence of mass curves the spacetime around the mass. The more massive the object the more curvature occurs, as Illustrated in the diagram below (The lines in this picture represents the path in which a light will travel on the curvature of space). As can be seen in this diagram the more massive body at the center has a deeper curvature while the less massive body at the edge has less of a curvature. Both, however, have a curvature, and these curvatures occur within each other. These curvatures are informally referred to as gravity wells. When mass or energy travels through these curves it follows a path of the curvature (this is why light bends when it passes near the Sun, as it is traveling on a curvature of space).
 One Body Curvature
|
 Two Body Curvature |
 Three Body Curvature |
This means that gravity is NOT a force as in the force of Electromagnetism, Strong Nuclear, and Weak Nuclear forces. The Electromagnetic, the Strong Nuclear, and the Weak Nuclear forces interact with each other and change the dynamics of each other. Gravity, however, just exists and objects simply move along the curvature of space in a path of least resistance. So why does gravity appear to be a force that attracts mass and energy? Let us take the example of a parachutist jumping out of an airplane. The parachutist looks down at the Earth and thinks he is being pulled down to the Earth, and a person on the Earth looks up at the parachutist and thinks that the parachutist is being pulled down to the Earth. But this is not what is happening from a gravitational perspective (there is no pulling force between the Earth and the parachutist). The parachutist has his own curvature of space, and the Earth has its own curvature of space, and both curvatures of space are within each other. The parachutist is actually moving on the path of least resistance inside the Earth’s curvature of space. As the Earth’s curvature of space is greater than the parachutist curvature of space the path of least resistance is toward the Earth’s center. If the parachutist closed his eye after jumping he would think that he is floating in space. He wouldn’t be aware, until he strikes the Earth, that there was any movement (or pulling). Therefore, no pulling is required for gravity to work, only the movement of objects within the curvature of space is required for gravity to work.
When bodies are within each other's curvature of space the lesser body will often revolve around the greater bodies curvature of space (technically they revolve around each other in an ellipse as Kepler stated in his first law of planetary motion). Einstein's field equations of general relativity can be utilized to accurately predict the motion of all bodies within the curvature of space.
It should be noted that when many nearby bodies are curving spacetime their gravitational wells overlap each other, and they interact with each other gravitationally. This affects the motion of the mass and light within the system as each body moves along the interacting curvatures, as seen below. This commonly occurs in multiple star systems. Another example is that the Moon’s gravity well is inside the Earth’s gravity well and that the Earth’s gravity well is inside the Sun's gravity well, and all three gravity wells are in each other’s gravity well. This interaction of the curvature of space affects the movements of the Moon, the Earth, and the Sun.
However, this representation is not entirely accurate as the curvature of space is in three dimensions, while the diagram is a two-dimensional representation of the effect. For a more accurate picture, you must imagine that the mass is located at the center of a three-dimensional sphere, and the gravity well existing on every point on the sphere.
The question arises that if a lesser massive body is revolving around a greater massive body why doesn't the lesser body spiral into the greater body. The answer to this question is that gravity is not the only force at work in this situation. When one body revolves around another body there is also another force called centrifugal force. If you imagine that you tied a ball to a long piece of string and started twirling it around your head and then released the string, the ball would fly away from you. It does so because of centrifugal force. In this example, the inward force preventing it from flying away is known as the centripetal force and is a result of your holding the string with your hand. The shorter the string and therefore the closer the ball is to your hand the faster the ball moves, and you must work harder to get the ball to revolve. Conversely, the further the ball is away from your hand the slower the ball revolves, and the less work is required to twirl the ball. This is as it is with a lesser body revolving around a greater body in space. The further out a lesser body is from the greater body the less centrifugal force it contains, and the further in the lesser body is from the greater body the more centrifugal force the lesser body has. The motion of one body around another body in space is a tug-of-war between the centripetal (gravitational) force and the centrifugal force. If the gravitational force is greater than the centrifugal force, then the lesser mass body will spiral into the greater mass body. If the centrifugal force is greater than the gravitational force, then the lesser mass body will spiral out of the greater mass body. If the centrifugal force and the gravitational force are equal, then one body revolves around the other body and neither spirals in nor spirals out.
During the early formation of the solar system, this spiraling in and spiraling out occurred on a regular basis. The objects that spiraled in were absorbed by the Sun, and the objects that spiraled out eventually ended up in the Kuiper Belt (a region of the solar system beyond the orbit of Neptune, believed to contain many comets, asteroids, and other small bodies made largely of ice) where the Sun’s gravitational force equals the bodies centrifugal force, or they were completely ejected from the Solar System's gravitational influence. The bodies left over in the Solar System became the moons, planets, minor planets, asteroids, and meteoroids that we see in the solar system today. But this spiraling does occur today and is mostly seen in the orbits of comets.
Many stars form in pairs or trinary systems in which the Stars revolve around each other’s curvature of space. When we observe these star systems we can often measure the spiraling of the stars within the system, and in many of these systems the stars within them spiral into each other and merge. We shall examine this effect in our topic on The Gravity of Stars.
The Geometry of Spacetime
General Relativity is also described as the curvature of spacetime. In mathematics, there are three types of curves; Flat, Spherical, or Hyperbolic. This allows for the Universe to have three different structures, with three different consequences as illustrated below. Astronomers have been trying to measure the Universe to determine its curvature, with current results indicating that we live in a flat universe.
An example of the consequences of this geometry is a thought experiment utilizing two parallel light beams. In a Flat universe, the light beams would never meet nor diverge and would proceed throughout spacetime as parallel beams to infinity. In a Spherical universe the initial parallel beams would eventually converge and cross over each other, and if you waited long enough, they would return to their point of origin as parallel beams. In a Hyperbolic universe, the beams would diverge in a gradual arc away from each other and would proceed throughout spacetime diverging to infinity.
The Gravity of Stars
When stars and solar systems are first formed the gravitational curvature of nearby space is responsible for the material (mostly hydrogen and helium) that is in nearby space to coalesce. As more and more material coalesce gravity becomes stronger. When gravity becomes strong enough the material is under so much gravitational pressure that the hydrogen and helium start to fuse and create heavier elements and release energy as part of this process. This entire process is called nucleosynthesis. Once nucleosynthesis starts the radiation pressure of energy escaping from the star counterbalances the gravitational force of the star. For the next hundreds of millions or billions of years there is a battle between the gravitational force trying to draw everything in, and the radiation force pushing everything out. This is a battle in which the gravitational force always wins. This is because as nucleosynthesis occurs there is less and less material (mainly hydrogen and helium) to create radiation pressure. Eventually, the radiation pressure is less than the gravitational force because of nucleosynthesis creating heavier elements and radiating away energy, and the stars life comes to its end phase. When this happens, the star blows off the gases surrounding it, and the mass of the star contracts and can end up in different forms. Stars of very low mass are known as Red Dwarfs in which the nucleosynthesis is so slow that they have lifetimes of trillions of years (greater than the age of our universe) and they simply dissipate over time. More massive stars have a different lifespan and ending. Depending upon the original mass of the star it can end up as a white dwarf, a neutron star, or a black hole.
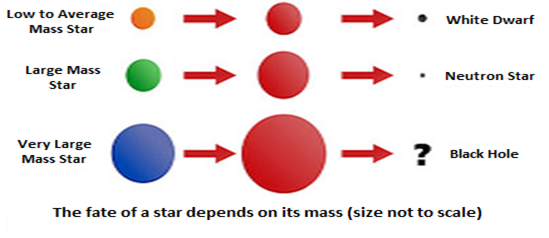
If the star is about the same mass as the Sun, it will turn into a white dwarf star. If it is somewhat more massive, it may undergo a supernova explosion and leave behind a neutron star. But if the collapsing core of the star is of very great mass -- at least three times the mass of the Sun -- nothing can stop the collapse. The star implodes to form an infinite gravitational warp in spacetime -- a black hole.
Low to average mass stars (Mass under 1.5 times the mass of the Sun) become White Dwarfs, while large mass stars (Mass between 1.5 to 3 times the mass of the Sun) become Neutron Stars. Very large mass stars (Mass over 3 times the mass of the Sun) become Black Holes.
Einstein’s General Relativity predicted the fate of a star based on its mass. It also predicted many other aspects of what happens after a star collapses. The more massive the star the greater the gravity well it forms and strange things happen within these gravity wells.
When stars collapse at the end of their lives relativistic effects become more apparent. General Relativity (and Special Relativity) always apply, but they become more noticeable and have a greater effect on the extremes of gravitational acceleration. And white dwarfs, neutron stars, and black hole are at the extremes. The gravitational depth of the well increases as more massive atoms are created because of nucleosynthesis. With this stellar collapse, gravity becomes stronger and the gravity well deepens. As always, any object that enters the gravity well that has less of a centrifugal force than the amount of gravitational force the object will be absorbed by the white dwarf, neutron star, or a black hole. If it's centrifugal force is greater than the gravitational force it will climb out of the gravity well and continue its trajectory. If the centrifugal force and the gravitational force are equal (very rare but mathematically possible) it will start a revolution around the white dwarf, neutron star, or a black hole that formed the gravitational well. This can be seen in the following diagram.
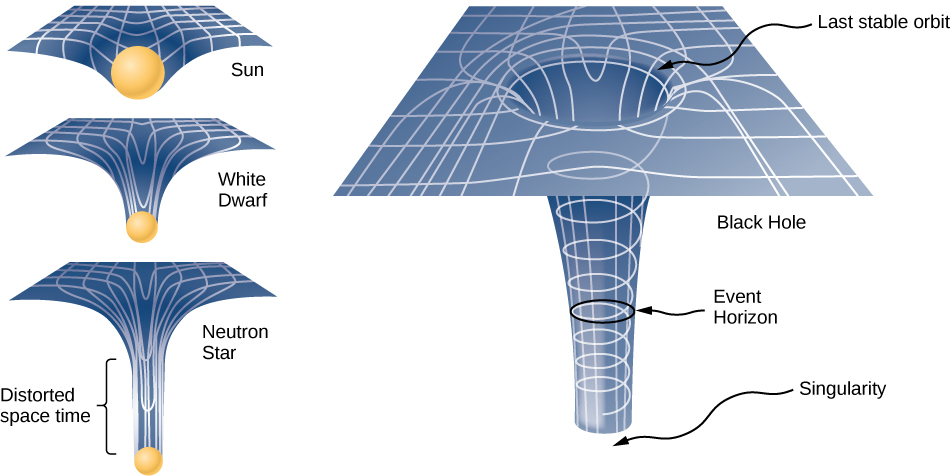
The first thing that happens in the creation of a white dwarf, neutron star or a black hole the effects of special relativity become more noticeable. As an object accelerates down the gravity well the effects of special relativity relativistic time and the relativistic length of the object changes. Its motion has the same trajectory as it follows the curvature of spacetime within the gravity well. However, it takes a longer time to complete its trajectory as the gravity well is deeper. As a white dwarf, neutron star, or a black hole starts spinning faster during the collapse other relativistic effects happen. The first is that magnetic pole of the white dwarf, neutron star, or a black hole may be different from the rotational pole of the star. When this happens, the star becomes a pulsar (see below). Also, the gravity well near the white dwarf or neutron star begins to twist slightly. This effect is not noticeable in a white dwarf as this effect is very small (but still there), but it can be visible if a neutron star has sufficient mass to make this detectable. Also, when the star collapses not all the matter is distributed equally in the star. Therefore, this unequal distribution produces a slight wobble. What this means is that the gravitational well not only deepens but it twists in the direction of the rotation. Any object that comes out of the gravitational well that has passed through this twist has a slightly different trajectory because of this twisting.
When a star becomes a black hole, however, there are many more relativistic effects. An object can revolve around a black hole if the orbit around the black hole is outside of its stable orbit diameter. However, if you go below the stable orbit diameter gravity becomes so strong that no matter what your centrifugal force you are trapped inside the black hole, as gravity is stronger than any centrifugal force. It is also not possible to apply addition acceleration (such as a rocket) to escape a Black Hole once you go below the stable orbit diameter (one of the consequences of acceleration of mass in Special Relativity). You begin to spiral down the gravity well until you reach the Event Horizon. Until you reach the Event Horizon it is possible for an observer to see you spiraling down the black hole. Once you reach the Event Horizon, however, gravity becomes so strong that not even light can escape the gravity well, and for all intents and purposes you wink out of existence. You do not actually wink out of existence, but nobody can see you, because light cannot escape the gravity well at the Event Horizon. However, after the Event Horizon is reached you will continue to spiral down the gravity well until you reach the singularity. In a singularity, the gravity is so strong, and quantum physics is so compressed, that the laws of physics no longer apply. At this point, you effectively no longer exist in our universe. The twisting of spacetime due to the rotation of the singularity is also present and observable above the Event Horizon.
All of the effects within the gravity wells of white dwarfs, neutron stars, or black holes can be accounted for by the field equations of General Relativity.
More information on these subjects can be found at the Wikipedia articles on:
Stellar Evolution, Red Dwarfs, White Dwarfs, Neutron Stars, and Black Holes.
Other Exotic Objects
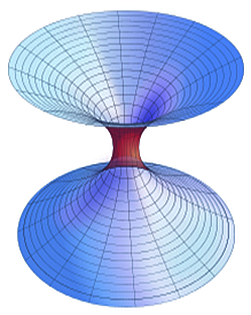 |
WormholesA wormhole is a concept that represents a solution of the Einstein field equations that is a complex structure linking separate points in spacetime. A wormhole can be visualized as a tunnel with two ends, each at separate points in spacetime (i.e., different locations and/or different points of time) Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist has not been proven. A wormhole, if they exist, could connect extremely long distances such as billions of light years or more, short distances such as a few meters, or different points of time (and distance). |
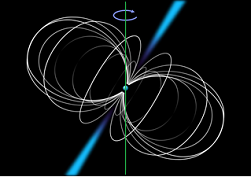 |
PulsarsA pulsar (from pulse and -ar as in quasar) is a highly magnetized, rotating neutron star or white dwarf, that emits a beam of electromagnetic radiation. This radiation can be observed only when the beam of emission is pointing toward Earth (much like the way a lighthouse can be seen only when the light is pointed in the direction of an observer) and is responsible for the pulsed appearance of emission. White Dwarfs and Neutron stars are very dense and have short, regular rotational periods. This produces a very precise interval between pulses that range from milliseconds to seconds for an individual pulsar. |
 |
QuasarA quasar is an extremely luminous active galactic nucleus (AGN). It is sometimes known as a quasi-stellar object, abbreviated QSO. This emission from an AGN is powered by a supermassive black hole with a mass ranging from millions to tens of billions of solar masses, surrounded by a gaseous accretion disc. Gas in the disc falling towards the black hole heats up because of friction and releases energy in the form of electromagnetic radiation. The radiant energy of quasars is enormous; the most powerful quasars have luminosities thousands of times greater than that of a galaxy such as the Milky Way. Usually, quasars are categorized as a subclass of the more general category of AGN. The redshifts of quasars are of cosmological origin. Hubble images of quasar 3C 273. At right, a coronagraph is used to block the quasar's light, making it easier to detect the surrounding host galaxy. The term quasar originated as a contraction of "quasi-stellar [star-like] radio source"—because quasars were first identified during the 1950s as sources of radio-wave emission of unknown physical origin—and when identified in photographic images at visible wavelengths, they resembled faint, star-like points of light. |
Gravitational Lenses
Just as starlight is deflected passing the sun, so should light from a distant galaxy be lensed when there is an intervening massive body such as a closer galaxy. This lensing is seen as a circle (often observer as arcs) around the intervening galaxy. The diagram below illustrates this phenomenon.
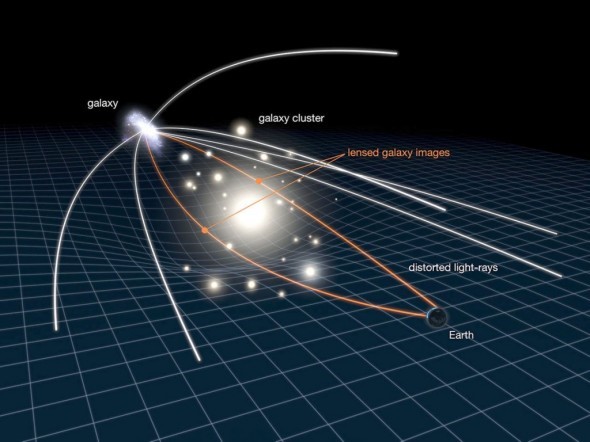
When the Hubble Space Telescope started imaging the universe in greater detail and was able to detect dimmer objects, it became possible to see Gravitational Lenses.

Astronomers are now able to discover farther galaxies being hidden by an intervening galaxy because of the detection of lensing. Astrophysicists can also analyze the lensed light and determine the properties of the far way galaxy being lensed.
Gravity Waves
One of the predictions of General Relativity is that if two massive objects revolve around each other and merge to become one object this merger would produce a ripple in spacetime named a gravitational wave. You may image a stone tossed into a pond that produces a wave that spreads outward throughout the pond. The gravitational wave would spread outward throughout the Universe. As gravity is a Universal Force (as opposed to the Electromagnetic, Strong and Weak forces which are localized) it spreads throughout the entire universe. This gravitational merging and the gravitational wave is Illustrated in the diagram below. Again, this is a two-dimensional representation of a three-dimensional phenomenon, but you can imagine a radio tower broadcasting a single, rather than a continuous radio wave in all directions. The duration of the gravity wave is usually under a few seconds.

As gravity is a universal force, it is also the weakest force in the universe. Scientist despaired of ever detecting gravitational waves because of the week nature of gravity. However, in the 1980s some scientists started trying to detect gravity waves. In this they were unsuccessful as the technology to detect gravity waves was not sufficient. However, in the early 1990s, a scientist thought that with the increased technological development of atomic clocks, lasers, computers, as well as construction techniques that it may be possible to detect gravity waves. This scientist convinced a board member of the National Science Foundation(NSF) that he could detect gravity waves. The board member pushed his proposal through the NSF despite objections from all the other members of the NSF. Their objections were that it would take many years to create this observatory, and it would be very expensive, the most expensive project ever funded by the NSF. This money and time that could be better spent on other scientific endeavors that were more likely to produce scientific results.
The board member was eventually able to push it through the NSF and 260 million dollars and five years were allocated to create this observatory, referred to as the Laser Interferometer Gravity Wave Observatory (LIGO). As with most government contracts it actually took 7 years and 320 million dollars to complete. At the end of this development, the scientists responsible for the LIGO realized that their experiment would not work, as the threshold for detecting gravity waves was lower than the threshold of their equipment. However, they believe that advances in the technology, and what they had learned from their LIGO observatory development could help them develop an advanced LIGO (aLIGO) that would be able to detect gravity waves. By this time the NSF member who had push through the original experiment was now the Chairman of the NSF, and he pushed through the funding to create an advanced LIGO, with a budget of 360 million dollars and seven years. Again, it took longer and more money to create this experiment, but at the end of the experiment, they succeeded. While in stage 4 of a 5-stage calibration process they detected a gravitational wave in January 2015. This gravitational wave was created by the merger of two black holes over 6 billion light-years away. Since that time, they have detected four other gravity waves, the last one being the merger of two neutron stars about 250 million light-years away. Because of their success, another aLIGO Observatory was built, and others are under construction or being planned for construction.
The success of aLIGO was very exciting and opens a new way to observe the universe. It has been likened to the development of sound in Motion Pictures. Prior to sound in Motion Pictures all you could see where the movement of what was being filmed. This produced dramatic moving images but not much in the way of storytelling or understanding of what was being filmed. Once sound was added to Motion Pictures the dramatic impact was immense, and motion picture technology and its usefulness increased dramatically. This is how it will be with LIGO. Prior to LIGO all that astronomers could observe were images of astronomical objects in the electromagnetic spectrum. With the success of aLIGO astronomers now have a tool in which they can hear the universe as they never could before. This could lead to revolutionary advances in astronomy.
The Laser Interferometer Gravitational-Wave Observatory (LIGO)
The Laser Interferometer Gravitational-Wave Observatory (LIGO) is a large-scale physics experiment and observatory to detect cosmic gravitational waves and to develop gravitational-wave observations as an astronomical tool. Two large observatories were built in the United States with the aim of detecting gravitational waves by laser interferometry. These can detect a change in the 4 km mirror spacing of less than a ten-thousandth the charge diameter of a proton, equivalent to measuring the distance from Earth to Proxima Centauri (4.0208x1013km) with an accuracy smaller than the width of a human hair.
The initial LIGO observatories were funded by the National Science Foundation (NSF) and were conceived, built, and are operated by Caltech and MIT. They collected data from 2002 to 2010 but no gravitational waves were detected.
The Advanced LIGO Project to enhance the original LIGO detectors began in 2008 and continues to be supported by the NSF, with important contributions from the UK Science and Technology Facilities Council, the Max Planck Society of Germany, and the Australian Research Council. The improved detectors began operation in 2015. The detection of gravitational waves was reported in 2016 by the LIGO Scientific Collaboration (LSC) and the Virgo Collaboration with the international participation of scientists from several universities and research institutions. Scientists involved in the project and the analysis of the data for gravitational-wave astronomy are organized by the LSC, which includes more than 1000 scientists worldwide, as well as 440,000 active Einstein@Home users as of December 2016.
LIGO is the largest and most ambitious project ever funded by the NSF.
As of August 2017, LIGO has made five detections of gravitational waves, the first four of which were colliding black-hole pairs. The fifth detected event, on August 17, 2017, was the first detection of a collision of two neutron stars, which simultaneously produced optical signals detectable by conventional telescopes.
How LIGO Works
A diagram of the LIGO observatory experimental equipment is as shown below. A brief description of how this works helps understanding of Gravity Waves work. A very short laser pulse is sent to a beam-splitting mirror where it is split into two beams at 90° angles and sent down a detector arm. At the end of the detector arm, another reflecting mirror reflects the laser light back to the beam splitting mirror, where it reflected to a light detector. In a normal situation, both laser beams should match in time when they meet at the light detector. However, if a gravity wave passes through a detector arm it will slightly expand and contract the detector arm, which changes the time it takes for the different laser beams to arrive at the light detector. This will cause the returning laser light to not match the time of return of the other detector arm laser light. When this happens the LIGO Observatory converts the mismatch of time into a chirp, alerting the experimenters that a gravity wave has been detected. The aLIGO Observatory must be located in a gravitational quiet zone so as to not have local gravitational interferences set off the detector. For many miles around the LIGO observatory, no transportation is permitted. This means that automobiles, trucks, trains, airplanes, or anything moving object that could produce a gravitational wave can that could set off the detection are not permitted in this quiet zone. It also means that no person can be present at the LIGO observatory, as their movement produces gravitational waves can set off the detector. As a result of no personnel allowed the entire operation of the LIGO Observatory is computer controlled. An aLIGO approved scientist or engineer that wishes to examine the LIGO results or equipment must log onto the computer remotely to look at the experimental results or equipment status.
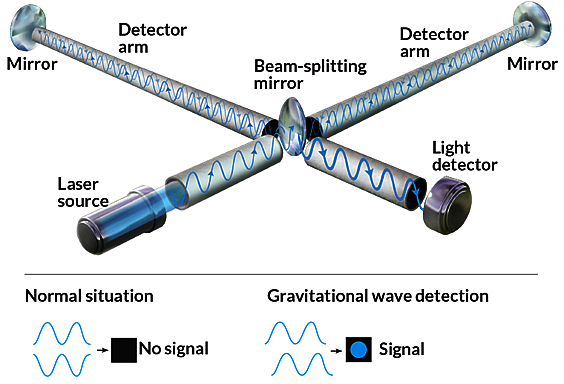
There must be a least two aLIGO observatories separated by thousands of miles, to separate local gravitational interferences from the cosmological gravitational waves. Initially, there were two observatories within the United States, and now there is a third Europe-based (located in Italy) observatory. Other aLIGO observatories are under construction or planned. The more observatories there are the greater the detection rate, and a more precise determination of the area of the heavens the gravity waves originated from. The determination of the location of the originating gravity wave is done by examining the times of arrival of the gravity ware at each observatory. The more aLIGO observatories there are the narrower the location of the originating gravity wave can be determined.
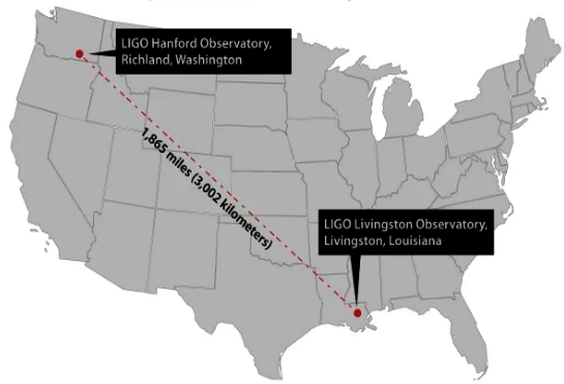
The Nobel Prize in Physics for 2017 went to Rainer Weiss, Barry C. Barish and Kip S. Thorne, the principal scientists and engineers responsible for the development of LIGO and aLIGO "for decisive contributions to the LIGO detector and the observation of gravitational waves". This was the shortest duration of a Nobel Prize from a discovery to the prize in the history of the Nobel Prize, which is an excellent indicator as to the importance of aLIGO to Cosmology.
For a more detailed (but understandable) explanation of Gravity Waves and how LIGO works please visit the LIGO Scientific Collaboration (LCS) website.
Cosmological Constant
In 1917, Albert Einstein inserted a term called the cosmological constant into his theory of general relativity to force the equations to predict a stationary universe in keeping with astrophysicists' thinking at the time. When it became clear that the universe wasn't actually static, but was expanding instead, Einstein abandoned the constant, calling it the '"biggest blunder" of his life.
But lately, scientists have revived Einstein's cosmological constant to explain a force that seems to be counteracting gravity (Dark Energy), causing the universe to expand at an accelerating pace.
A new study confirms that the cosmological constant is the best fit for dark energy and offers the most precise and accurate estimate yet of its value. The finding comes from a measurement of the universe's geometry that suggests our universe is flat, rather than spherical or curved.
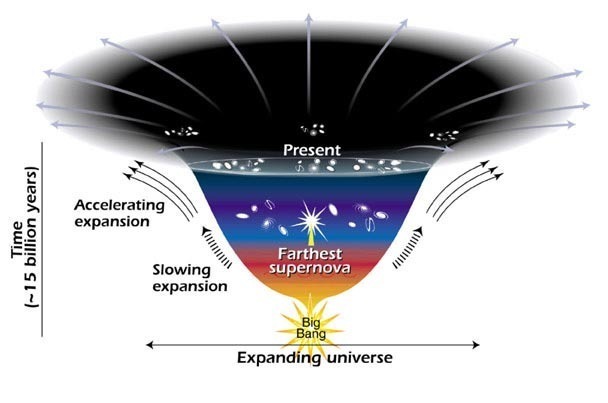
As a result of this measurement, we now know that the universe will expand forever, and all the matter and energy will decay into free sub-atomic particles, and the universe will die a thermodynamic death (free sub-atomic particles have no interactions with each other).
Dark Matter & Dark Energy
In 1922 Jacobus Kapteyn suggested the existence of dark matter, using his studies of stellar velocities. In 1933 astrophysicist Fritz Zwicky, who studied galactic clusters, made a similar inference. In 1978 Vera Rubin and W. Kent Ford confirmed the existence of Dark Matter in nearby galaxies using galaxy rotational curves. In the early 1990’s Astrophysicists verified the existence of Dark Matter throughout the universe. This was done by utilizing space telescopes to take a census of the stars and their star type in many galaxies to determine the approximate mass of the galaxy. They then measured the motion of selected stars through the galaxy. They entered this information into a supercomputer that utilized Einstein’s General Relativity equations to produce a gravitational model of the galaxy. To their surprise, the model said that all the Galaxies they studied could not exist because there was insufficient mass to hold them together. They adjusted the amount of mass in the galaxies in such a manner as to get the result that agreed with what they were observing in galaxies. In every case the adjustment was the same – the amount of normal matter (baryonic matter) was 20% of what was needed while 80% of the matter was unseen – which they named “Dark Matter”.
In the late 1990’s Astrophysicists realized it would be possible to measure the rate of expansion of the universe utilizing space telescopes and supercomputers (again utilizing Einstein’s General Relativity equations). At that time, they had three scenarios as to the ultimate fate of the universe; a closed universe, an open universe, or a flat universe. A closed universe is one in which the mass of the universe was greater than the force of expansion, and the universe would collapse onto itself to create a new universe (the expansion of space, a stop, and then the contraction of space). An open universe is one that the expansion is greater than the mass and the universe will expand forever and eventually suffer total radioactive decay and cease to exist. A flat universe is one in which the mass and the expansion are equal, and the universe would just stop and be fixed in size (nobody expected this result, but it was possible mathematically). Everybody expected that the rate of expansion was slowing, and we would end up in either an open or closed universe. To their surprise, the results showed that the rate of expansion was increasing. The only way this would be possible if there were a repulsive energy force that was greater than the gravitational force. They named this energy “Dark Energy”.
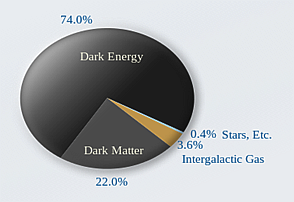 |
Given what we now know we can confidently say that about 74% of the Universe is composed of Dark Energy, and about 22% of the Universe is composed of Dark Matter, while only 4% of the Universe is Baryonic matter. This means that the “Standard Model of Quantum Physics” only accounts for 4% of what the universe is composed of. This situation, along with the unification of General Relativity and Quantum Physics, needs to be rectified to have a fuller understanding of how and why the Universe works. |
The existence of Dark Matter and Dark Energy had no impact on General Relativity, as the equations of General Relativity allowed for their existence. Indeed, by including Dark Matter and Dark Energy into Einstein’s equations we have a much better understanding of how our universe works gravitationally.
Additional Thoughts
The Three Body Problem
Chaos, Complexity, and Networks
What are chaos, complexity, and network science, and what does it have to do with this subject. Directly Everything and Indirectly Everything!
When three or more bodies (3-body or n-body) are revolving around each other gravitationally it becomes very difficult and complex to calculate the orbits of the bodies. Newton’s Universal Gravitation theory can be used to do the calculations, but this is difficult and complex mathematics and the results are inaccurate due to the theory being incorrect. Utilizing Einstein’s correct General Relativity Theory leads to accuracy, but as Einstein’s field equations are very complex and the mathematics is very difficult to calculate.
Below is the Newtonian explanation of the 3-body problem and solution.
 |
In physics and classical mechanics, the Three Body Problem is the problem of taking an initial set of data that specifies the positions, masses, and velocities of three bodies for some particular point in time and then determining the motions of the three bodies, in accordance with Newton's laws of motion and of universal gravitation which are the laws of classical mechanics. The three-body problem is a special case of the n-body problem. Unlike two-body problems, there is no general closed-form solution for every condition, and numerical methods are needed to solve these problems. |
Historically, the first specific three-body problem to receive extended study was the one involving the Moon, the Earth, and the Sun. In an extended modern sense, a three-body problem is a class of problems in classical or quantum mechanics that models the motion of three particles.
The Einsteinian solution is so complex that it cannot be diagrammed, and the equations run for several pages of intricate mathematics. However, modern supercomputers have made these calculations possible. Using supercomputers the Einstein 3-body can be solved in a few hours, but a n-body solution on a supercomputer can take days or weeks depending on the number (n) of bodies.
Utilizing the supercomputers calculations and graphics capabilities scientists can produce the following visualization of a simple 3-body problem. The Vimeo video simulation of the solution is amazing, and you should examine this video.
There is, however, another problem in obtaining accurate results to the 3-body or n-body problem. This is the problem of “Chaos”, “Complexity”, and “Networks”. In the last several decade's scientists have discovered and developed the science of chaos, complexity, and networks. This discovery and development were very important, as it explained why some scientific observations and experiments did not conform to expectations but varied, sometimes significantly, from what they expected. It also explained why scientific predictions in computer modeling would always contain inaccuracies.
If you are going to create, develop or utilize scientific and engineering studies you need to be aware of chaos, complexity, and network science. You first need to understand something of chaos, complexity and network science to understand their impact on this subject. For this understanding, I have prepared another article “Chaos, Complexity, and Network Science” that I would direct you too. Briefly, however, Chaos, Complexity, and Networks Science is as follows:
Chaos theory is the field of study in mathematics and science that studies the behavior and condition of dynamical systems that are highly sensitive to initial conditions, a response popularly referred to as the butterfly effect (Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?). Small differences in initial conditions (such as those due to rounding errors in numerical computation) yield widely diverging outcomes for such dynamical systems, rendering long-term prediction impossible in general.
Complexity characterizes the behavior of a system or model whose components interact in multiple ways and follow local rules, meaning there are no reasonable means to define all the various possible interactions. Complexity arises because some systems are very sensitive to their starting conditions so that a tiny difference in their initial starting conditions can cause big differences in where they end up. And many systems have a feedback into themselves that affects their own behavior, which leads to more complexity.
Network science studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks. Distinct elements or actors represented by nodes, and the links between the nodes, define the network topology. A change in a node or link is propagated throughout the network and the Network Topology changes accordingly. Network science draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology.
Gravity and The Three Body Problem:
In the Network of our Solar System and its Planets Einstein’s General Theory of Relativity can predict the revolutions of the Planets around the Sun. However, the Planets interact gravitationally with each other as well as with the Sun. As the precise gravitational figures of the Sun and Planet Masses, as well as the precise distances between the Sun and the Planets, and the precise velocities of the Planets are not known, the Network becomes unstable. As Complexity builds up Chaos will be the result, and our predictions of the orbits will fail. The actual Planetary orbit can also change due to unknown, unnoticed or unaccounted for factors (such as minor planets, asteroids, meteorites, comets, or another unknown mass passing by our Solar System). Our predictions are accurate for tens or hundreds of millions of years, but sometime in that timescale the orbital prediction will no longer be accurate. The Planetary actual orbits can also change due to the unknown, unnoticed or unaccounted factors. Thus, Network science, Chaos and Complexity is embodied in our Solar System in a both a predictive and actual manner.
The Birth of Gravity
Not until Big Bang and Quantum theory were developed was it possible to explain how gravity was born. We now know that the four forces of nature evolved it the first second of the creation of the universe. We also know how gravity helped shape the structure of the universe.
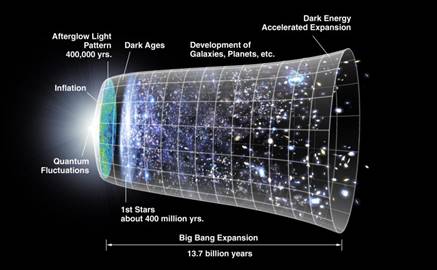
It wasn't until the 20th century when scientists combined general relativity with the expansion of the universe that they come up with the Big Bang Theory. As scientist realized the universe was expanding, and General Relativity could be used to understand this expansion, they realized that the Universe must have started with an incredibly dense and Incredibly small point. This point was named the Singularity, and it contained everything that is in our universe inside of it, but not in a manner that science could explain, and the four forces of nature did not yet exist. As everything was altogether in this singularity there were no physical laws or forces as we understood them. Soon after the eruption of the singularity, the four forces began to separate, with gravity becoming the first force to separate, and thus gravity was born.
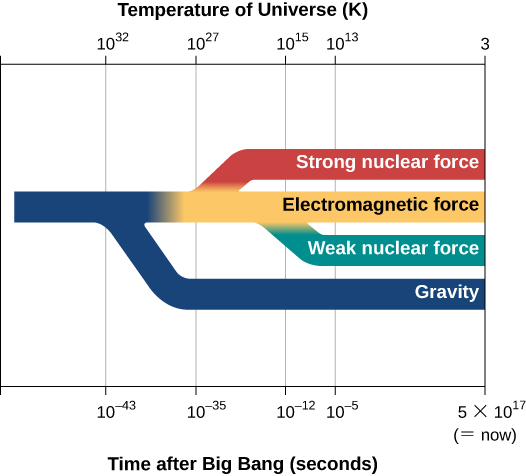
How Did All This Happen?
Where and how were the four forces of the universe created? The answer is in the initial creation of the Universe via the “Big Bang”.
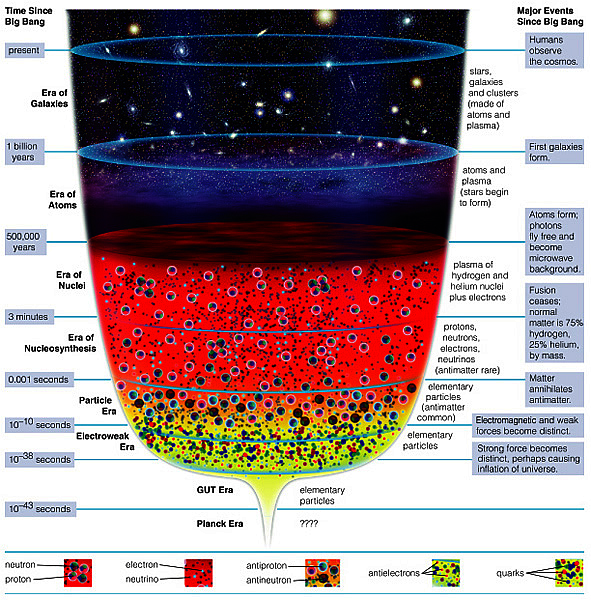
In the very beginning, everything in the Universe was compressed into a space the size of a subatomic particle named the Singularity which erupted. The four forces of the universe were one force, and the temperature and density were so unimaginably high that the current laws of physics were inapplicable. This was called Plank space and it is inexplicable. However, starting with the Grand Unifying Theory (GUT) period scientists were able to explain the timeline of the Big Bang, and the physical laws and forces within the Big Bang. Scientists are still looking for theories that could help explain what caused the eruption of the singularity.
During this eruption, the first subatomic particles that make up matter and energy were created. Space and time were born, and the cosmic clock started to run. At first, the Universe was extremely hot and dense with stuff flying in all directions with unimaginable speed. Scientists call this the inflationary epoch. In less than a millionth of a second, the Universe expanded from the size of a subatomic particle to a trillion times bigger than the Solar System. At this time the Universe was almost smooth and expanding symmetrically in all directions. However, astronomers think that small clumps in density caused the formation of the first stars and galaxies. The first few seconds were so hot that the four basic forces (Gravity, Electromagnetic, Strong Nuclear, and Weak Nuclear) were unified. Gravity was the first force to separate itself from the other forces. Next, the weak nuclear force split from the others, allowing the formation of the first quarks, the building blocks of subatomic particles. Later on, the strong force split off from the electromagnetic force and the first protons and neutrons were formed. After 100 seconds, it was cool enough for the first protons and neutrons started to link, however, the first atoms were very unstable and quickly broke apart. After three minutes the temperature dropped to a billion degrees and hydrogen and helium atoms formed. At the end of the Radiation era, the temperature dropped to 10,000K and the Universe became transparent in the Electromagnetic spectrum. A billion years later, the first stars and protogalaxies were formed.
Most people when they envision the Big Bang often think of it in an incorrect manner. They often envisioned looking at a small point of light that instantaneously becomes a tennis ball size of bright light. The next moment it becomes the size of a large geodesic dome of bright light, and from there they imagined it slowly expands to become the size of our universe. This, however, is not a good way of thinking about it. The reason for this is that you are imagining yourself outside of the small point of light. But as there is no outside so you cannot think of yourself as outside, you must think as if you were inside the point of light.
A better way to think of this is to imagine yourself in a very small and very dark cramped coffin (the singularity). All of the sudden the coffin becomes bright that is the size of the Earth (the tennis ball analogy). This happened so fast that you could not possibly know that it was happening. An instant later, so fast that you didn’t know it happened, it becomes the size of the Sun (the geodesic dome analogy), and then from there it slowly expanded to the size of the today's Universe.
But this way of envisioning is not quite correct because you always envision yourself at the center of this expansion. We must also add another way of thinking about the expansion. Think of an uncooked loaf of bread which has raisins randomly spread throughout it. After putting the loaf of bread in an oven and heating it up the bread starts to expand, and the raisins move away from each other as part of the expansion of the loaf of bread. Now imagine yourself standing on one of those raisins inside the loaf of bread. If you looked at the other raisins, no matter in which direction you looked, it would appear that the other raisins are moving away from you, and you are the center of this movement away. However, if you had a friend standing on another raisin nearby and shouted to ask him why he was moving away from you, he would look at all the other raisins and it would seem to him that the other raisins were moving away from him. He would shout back that he is not moving, and that you are moving away from him. You would then get into an argument about who is moving away from whom. The answer to this argument is that the raisins are not moving, but the space between them is increasing. This provides the illusion that everything is expanding around an individual raisin, and that each raisin thinks the other raisin is moving away from them. By combining the coffin envisioning with the raisin envisioning you get a better impression of what the Big Bang looked like.
The Size of the Universe
The next additional thought is What is the Size of the Universe? With the Big Bang occurring about 14 billion years ago does that mean that the universe is 14 billion light years in diameter? Well - No! When we look out to the universe we can see objects as far away as 14 billion light-years away, but we can see these objects in any direction that we look. Therefore, our observable universe is 28 billion light years in diameter. So, does that mean that the universe is 28 billion light years in diameter? Well - No! The problem is that we only appear to be in the center of the universe. If we harken back to our raisin bread analogy all the other raisins appear to be in the center of (their) observable universe. As there are many raisins in the loaf of bread they each can see an observable universe of 28 billion light years in diameter. Therefore, we get the situation as illustrated below.
My observable universe is the white and black shaded circle. Friend A’s Observable Universe is his grey shaded circle and my white area to the left of My Center, while Friend B’s Observable Universe is his grey shaded circle and my white area to the right of My Center. However, the black shaded area in My Observable Universe is not visible to either Friend A or Friend B. In addition, the grey shaded area of both Friend A and B is not visible to me, nor can Friend A see Friend B observable universe and vice-versa. So, does that mean that the universe is 56 billion light years in diameter? Well - No! There are also friends on all the other raisins with their own Observable Universe that may or may not overlap with others Observable Universes. And this overlap does not have to be based on a 14 billion light year distance between friends, as the friends can be any number of billions (or millions) of light years apart from each other with their own bubble.
We can think of this situation as one huge bubble (The Entire Universe) that has many 28 billion diameter Observable Universes bubbles within it. The question then is what is the size of the “The Entire Universe”?
We will never know by observing and measuring the Entire Universe, as the Entire Universe can never be visible to us. However, since we know when the Big Bang started, and when and the duration and the rate of the slowing expansion period of the universe, and when and the duration of the rate of the accelerating expansion period of the universe, it is possible to mathematically calculate the size of the Entire Universe. However, there are many different methods used to calculate the size of the Entire Universe, with varying (sometimes widely varying) results. As the numbers that go into these calculations are not precisely known these calculations are a guesstimate. Our best guesstimate, based on the most accepted method, is that the size of the entire universe is approximately 91 billion light years in diameter.
Instead of taking one measurement method, a team of scientists at the University of Oxford did a statistical analysis of all of the results. They utilized the Bayesian model averaging technique, which focuses on how likely a model is to be correct given the data, rather than asking how well the model itself fits the data, and they calculated another result. They found that the universe is at least 250 times larger than the observable universe, or at least 7 trillion light-years across.
The Problems with Gravitational Physics!
None – General Relativity has withstood every observation and experiment intact. The problem that exists is how to combine General Relativity with the Standard Model of Quantum Physics. While the Standard Model is a triumph of quantum physics and has withstood all observations and experimental tests, there are three major problems with the Standard Model as an explanation of how the Universe works.
The first is the problem of Gravity. Gravity is a universal force, but the “Standard Model” has no explanation for gravity, and gravity cannot incorporate the “Standard Model”. Until Gravity and the “Standard Model” can be incorporated (through a “Grand Unified Theory” – GUT) it is not possible to have a full understanding of how and why the Universe works.
The second is the problem of Dark Matter. When Dark Matter was discovered the astrophysicists went to the quantum physicists to ask what this Dark Matter could be. The quantum physicists had no answer. Yet everyone agrees that Dark Matter exists, and until the “Standard Model” can incorporate Dark Matter it will be incomplete.
The third is the problem of Dark Energy. When Dark Energy was discovered the astrophysicists went to the quantum physicists to ask what this Dark Energy could be. The quantum physicists had no answer. Yet everyone agrees that Dark Energy exists, and until the “Standard Model” can incorporate Dark Energy it will be incomplete.
Final Thoughts
The modern technological world is not possible without General Relativity and Quantum Physics. All modern electronics must take into account General Relativity and Quantum Physics to function properly. The ubiquitous cell phone electronics would not work without accounting for General Relativity for the Global Positioning System (GPS), and Quantum Physics in its electronics. Indeed, today’s world would not be recognizable without General Relativity and Quantum Physics. We all owe a debt of gratitude to all those thousands of Physicists who were involved in the discovery and development of General Relativity and Quantum Physics.
Further Readings
Below are the books I would recommend that you read for more background information on these scientists. They were chosen as they are a fairly easy read for the general public, and have a minimum of The Clockwork Universe: Isaac Newton, the Royal Society, and the Birth of the Modern World by Edward Dolnick
- Galileo: Decisive Innovator by Michael Sharratt
- The Life of Isaac Newton by Richard S. Westfall
- Einstein – His Life and Universe by Walter Isaacson
- What is Relativity by Jeffrey Bennett
- The Perfect Theory by Pedro G. Ferreira
- The Scientific 100 – A Ranking of the Most Influential Scientists, Past and Present by John Simmons
For a brief introduction on these topics I would recommend the Oxford University Press series “A Very Short Introduction” on these subjects:
- Gravity: A Very Short Introduction by Timothy Clifton
- Cosmology: A Very Short Introduction by Peter Coles
- Astrophysics: A Very Short Introduction by James Binney
For some videos on these topics I would recommend:
- Isaac Newton's World of Physics
- The Extraordinary Genius of Albert Einstein
- The Amazing World of Gravity
Some interesting website with general scientific topics are:
- Ask a Mathematician / Ask a Physicist
- Ask the Physicist!
- Physics and Astronomy Ask the Experts
- The Skeptic's Dictionary
- Understanding Science – how science really works
Timeline of Gravitational Physics and General Relativity
384 - 322 BC: Aristotle Geocentric Theory [Earth centered universe] and Motion.
310 - 230 BC: Aristarchus Heliocentric Theory [Sun centered universe].
287 - 212 BC: Archimedes Criticized Aristarchus' Discovery [The Sand Reckoner].
85-165 AD: Claudius Ptolemy – Mathematician and Astronomer who developed Epicycle Theory and Star Chart.
150 AD: Claudius Ptolemy - The Almagest first published.
1473 - 1543: Nicholas Copernicus - Developer of modern Heliocentric theory.
1543 - Nicolaus Copernicus “On the Revolutions of the Heavenly Spheres” published.
1546 -1601: Tycho Brahe - Naked-eye Astronomer who drew a comet by hand on 1577and witnessed a supernova [De Nova Stella]. Created the greatest naked-eye catalog of the position of the stars, and the positions of the movements of planets.
1564 - 1642: Galileo Galilei - Confirmed Copernicus' Heliocentric Theory via telescope observations and thought experiments. Studied the motions of moving bodies that disproved Aristotelian motion.
1571 - 1630: Johannes Kepler – Mathematician and Astronomer - Kepler's mathematical and astronomical work, alongside Brahe's planetary movement positions, resulted in the Three Laws of Planetary Motion.
1604 - Galileo Galilei conducts experiments with inclined planes and induces the law of falling objects.
1609 - Johannes Kepler describes the first two laws on the motion of planets around the Sun, now known as Kepler's Laws of Planetary Motion, in “Astronomia nova” (New Astronomy).
1619 - Johannes Kepler describes his third law of Planetary Motion in “Harmonices Mundi” (Harmony of the Worlds).
1610 - Galileo Galilei “The Starry Messenger” published.
1632 - Galileo Galilei “Dialogue Concerning the Two Chief World Systems” published.
1638 - Galileo Galilei “Discourses and Mathematical Demonstrations Relating to Two New Sciences” published.
1642 - 1727: Isaac Newton - Inventor of Calculus; Universal Law of Gravitation; the Three Laws of Motion; Master of Alchemy; Discovered Optics - and the Visible Light Spectrum. Using "mirror" technology to reflect light he invented the modern Telescope, which is still used planet-wide today.
1671 - Isaac Newton - Method of Fluxions (Calculus) completed.
1684 - Gottfried Leibniz "New method for maxima and minima, and for tangents, that is not hindered by fractional or irrational quantities, and a singular kind of calculus for the above mentioned." – the “Calculus” is published.
1687 - Isaac Newton “Mathematical Principles of Natural Philosophy” the “Principia” first published.
1705 - Edmund Halley - Influenced by Newton's calculations, predicted "Halley's Comet”.
1736 - Isaac Newton - Method of Fluxions (Calculus) published posthumously in 1736.
1831-1879: James Clark Maxwell - Physicist and Mathematician, formulated Electromagnetic theory.
1862 – Alvin Clark first White Dwarf star (Sirius B) discovered.
1855 – Urbain Le Verrier observes a 35 arcsecond per century excess precession of Mercury's orbit and attributes it to another planet, inside Mercury's orbit.
1879-1955: Albert Einstein - Special Theory of Relativity, General Theory of Relativity [included Gravity]; and Quantum Physics.
1882 - Simon Newcomb observes a 43 arcsecond per century excess precession of Mercury's orbit.
1905 - Albert Einstein completes his theory of special relativity and states the law of mass-energy conservation: E=mc2.
1907 - Albert Einstein introduces the principle of equivalence of gravitation and acceleration, and the bending of starlight.
1915 - Albert Einstein completes his theory of General Relativity.
1915 - Karl Schwarzschild predicts Black Holes based on Einstein’s Special Theory of Relativity.
1916 – Albert Einstein predicts massive objects whirling in certain ways will cause spacetime ripples—gravitational waves.
1919 - Arthur Eddington leads a solar eclipse expedition which detect gravitational deflection of light by the Sun, proving Einstein’s General Theory of Relativity.
1922 - Jacobus Kapteyn first suggests the existence of Dark Matter, using stellar velocities. In 1933, astrophysicist Fritz Zwicky, who studied galactic clusters made a similar inference.
1924 - Edmund Hubble proves the existence of Galaxies outside of the Milky Way.
1927 - Georges Lemaitre presented his idea of an expanding universe, derived from General Relativity and later known as Hubble's law, and provided the first estimation of the Hubble constant.
1929 - Edmund Hubble proves the expansion of the universe by measuring the redshifts of Galaxies.
1931 - Georges Lemaitre proposed what became known as the Big Bang theory of the origin of the universe, which he called his "hypothesis of the primeval atom" or the "Cosmic Egg".
1931 - Georges Lemaitre was the first scientist to propose the expansion of the universe was actually accelerating, which was confirmed observationally in the 1990s.
1934 - Walter Baade and Fritz Zwicky proposed the existence of Neutron Stars.
1937 - Fritz Zwicky states that galaxies could act as gravitational lenses.
1964 - Arno Penzias and Robert Wilson discover Cosmic Microwave Background (CMB), the remnants of the "Big Bang" which proves The Big Bang Theory.
1965 - Antony Hewish and Samuel Okoye discovered "an unusual source of high radio brightness temperature” in the Crab Nebula, which becomes the first Neutron Star discovered.
1966 - 1975 Stephen Hawking publishes a series of papers on Black Holes, Singularities, Spacetime, and Quantum Gravity and Quantum Mechanics.
1967 - Jocelyn Bell and Antony Hewish discover Pulsars.
1969 - Joseph Weber reports observation of gravitational waves (a claim now generally discounted).
1971 - Cygnus X-1, the first black hole found, is discovered by Uhuru satellite.
1976 - Gravity Probe A experiment confirmed slowing the flow of time caused by gravity matching the predicted effects to an accuracy of about 70 parts per million.
1978 - Vera Rubin and W. Kent Ford confirmed existence of Dark Matter in nearby galaxies using galaxy rotational curves.
1990’s - Verification of Dark Matter existence throughout the universe.
1998 - Adam Riess, Saul Perlmutter and Brian Schmidt discover Dark Energy, and reintroduce the “Cosmological Constant” into “General Relativity”.
2002 - First data collection of the Laser Interferometer Gravitational-Wave Observatory (LIGO).
2015 - Advanced LIGO reports the first direct detections of gravitational waves.
Disclaimer
Please Note - many academics, scientist and engineers would critique what I have written here as not accurate nor through. I freely acknowledge that these critiques are correct. It was not my intentions to be accurate or through, as I am not qualified to give an accurate nor through description. My intention was to be understandable to a layperson so that they can grasp the concepts. Academics, scientists, and engineers entire education and training is based on accuracy and thoroughness, and as such, they strive for this accuracy and thoroughness. I believe it is essential for all laypersons to grasp the concepts of this paper, so they make more informed decisions on those areas of human endeavors that deal with this subject. As such, I did not strive for accuracy and thoroughness, only understandability.
Most academics, scientist, and engineers when speaking or writing for the general public (and many science writers as well) strive to be understandable to the general public. However, they often fall short on the understandability because of their commitment to accuracy and thoroughness, as well as some audience awareness factors. Their two biggest problems are accuracy and the audience knowledge of the topic.
Accuracy is a problem because academics, scientist, engineers and science writers are loath to be inaccurate. This is because they want the audience to obtain the correct information, and the possible negative repercussions amongst their colleagues and the scientific community at large if they are inaccurate. However, because modern science is complex this accuracy can, and often, leads to confusion amongst the audience.
The audience knowledge of the topic is important as most modern science is complex, with its own words, terminology, and basic concepts the audience is unfamiliar with, or they misinterpret. The audience becomes confused (even while smiling and lauding the academics, scientists, engineers or science writer), and the audience does not achieve understandability. Many times, the academics, scientists, engineers or science writer utilizes the scientific disciplines own words, terminology, and basic concepts without realizing the audience misinterpretations, or has no comprehension of these items.
It is for this reason that I place understandability as the highest priority in my writing, and I am willing to sacrifice accuracy and thoroughness to achieve understandability. There are many books, websites, and videos available that are more accurate and through. The subchapter on “Further Readings” also contains books on various subjects that can provide more accurate and thorough information. I leave it to the reader to decide if they want more accurate or through information and to seek out these books, websites, and videos for this information.
If you have any comments, concerns, critiques, or suggestions I can be reached at mwd@profitpages.com.
I will review reasoned and intellectual correspondence, and it is possible that I can change my mind,
or at least update the content of this article.



 Stjerneborg
Stjerneborg